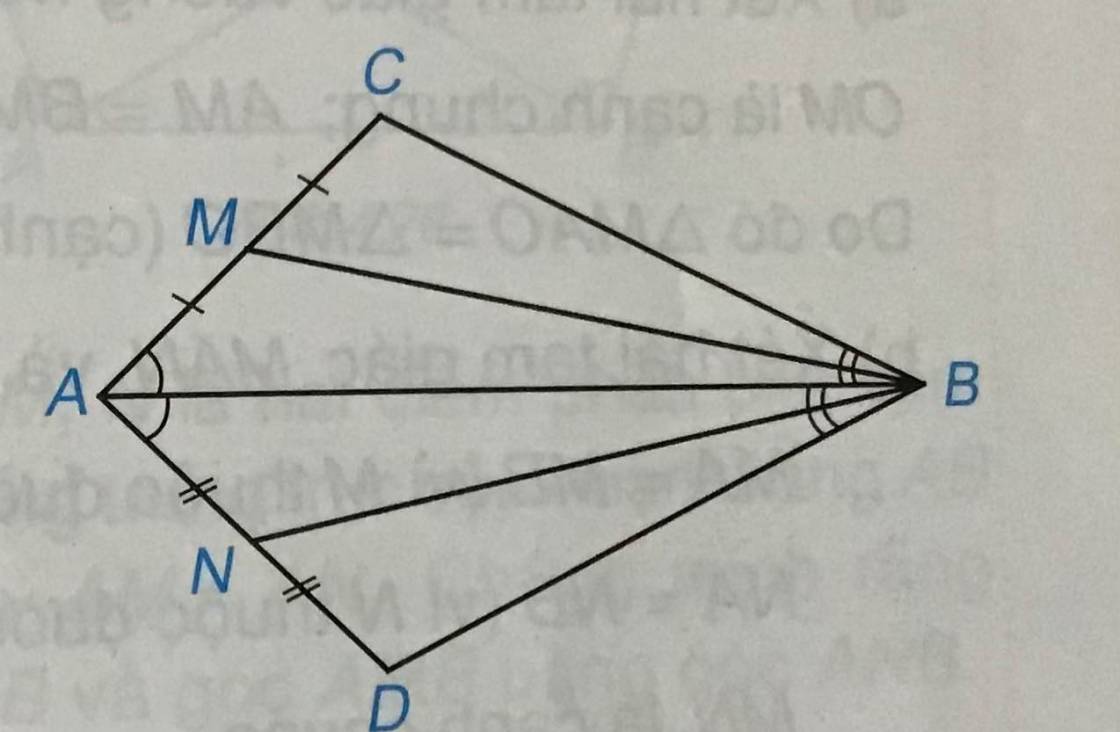
Câu a) đổi thành CM: MN//AB ; Câu d) đổi thành .......là trung điểm của AB....... nhé 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CI
0
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 12 2023
Xét \(\Delta\)ABC và \(\Delta\) ABD ta có: AB chung;
góc ABC = góc ABD
góc CAB = góc DAB
⇒ \(\Delta\) ABC = \(\Delta\) ABD (g-c-g)
⇒ BC = BD
AC = AD
BC = BD ⇒ \(\Delta\) CBD cân tại B mà AB là phân giác của góc CBD nên
⇒ AB là trung trực của CD vì trong tam giác cân đường cao cũng là đường trung trực, đường phân giác.
b, Xét \(\Delta\) ACD có
AM = AC;
AN = ND
⇒ MN là đường trung bình của tam giác ACD
⇒ MN//CD (đpcm)
c, AC = AD (cmt)
⇒ AN = AM = \(\dfrac{1}{2}AC\)
Xét tam giác AMB và tam giác ANB ta có:
AB chung; AN = AM
góc NAB = góc BAM
⇒ \(\Delta\) AMB = \(\Delta\) ANB (c-g-c)
⇒ Góc AMB = góc ANB (đpcm)
18 tháng 10 2019
a)xét tứ giác AMNH có:
góc HMA= 90 độ
góc HNA = 90 độ
góc MAH= 90 độ ( tam giác ABC vuông tại A)
=> AMHN là hình chữ nhật
=> AH=MN( tính chất 2 đường chéo)
18 tháng 10 2019
tứ giác AMHN có \(\widehat{A}\)=\(\widehat{M}\)=\(\widehat{N}\)=90\(^o\)
nên AMHN là hcn => AH=MN
7 tháng 11 2015
câu 1 : khi M nằm giữa A và B
câu 2;
b, Vì trên đoạn thẳng AB lấy điểm M => M nằm giữa A và B
=> AM + MB + = AB
AM = 2cm, AB = 6cm
=> MB = AB - AM = 6cm - 2cm = 4cm
b, Vì: N là tia đối của tia BM => B nằm giữa M và N
=> MB + BN = MN
MB = 4cm; BN = 2cm => MN = 4cm + 2cm = 6cm
c, Vì: AB = 6cm; MN = 6cm
=> AB = MN ( 6cm = 6cm )