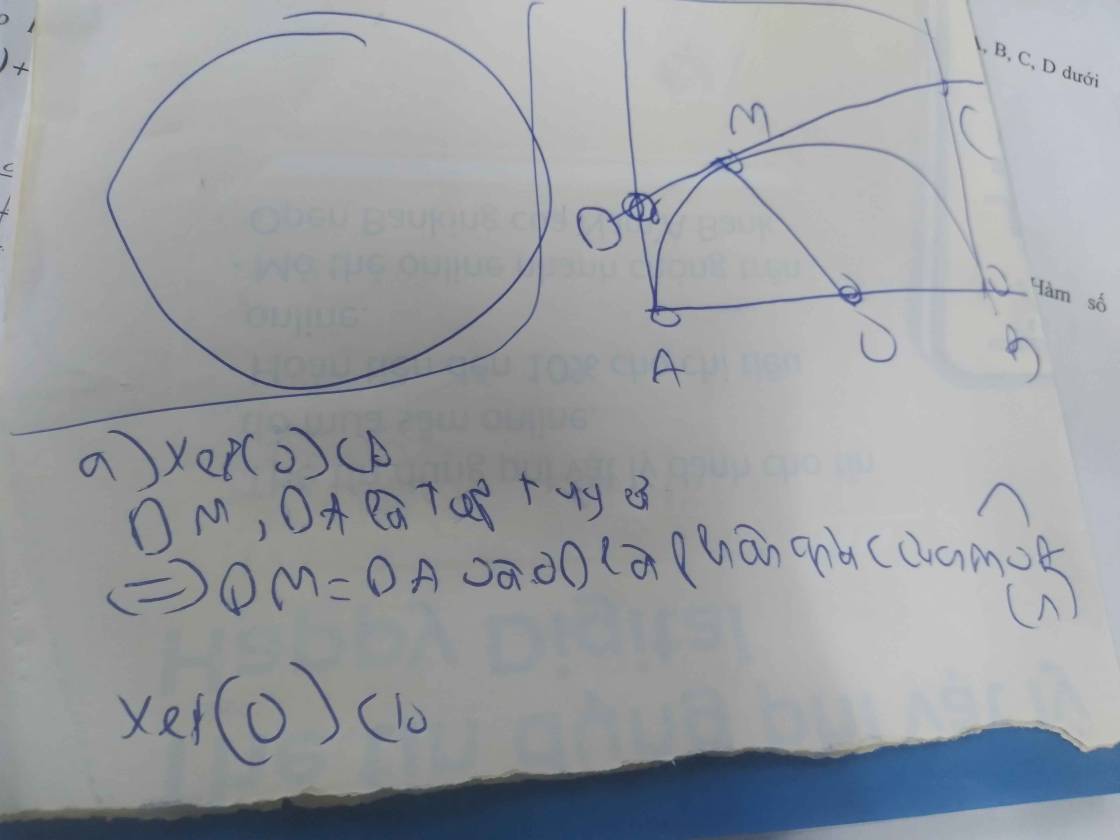
Cho nữa đường tròn tâm O đường kính AB=8cm. Vẽ \(\widehat{BAx}\)= \(^{60^0}\) cho cắt nửa đường tròn \((O)\) tại C.
a/ Tính AC,BC
b/ Tại C, vẽ tiếp tuyến d của nửa đường tròn \((O)\). Kẻ BD và AE lần lượt vuông góc với D \((D,A\in d)\)Chứng minh DE=BC
c/ Tính diện tích tứ giác AEDB
d/ Gọi K là giao điểm của EB và AC. Chứng ming \(\frac{1}{AK}\text{=}\frac{1}{AE}+\frac{1}{AB}\)