Cho x,y,z>0. CM: \(\dfrac{xy}{z^2\left(x+y\right)}+\dfrac{yz}{x^2\left(y+z\right)}+\dfrac{zx}{y^2\left(z+x\right)}\ge\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 2 2019
Sửa lại đề: cho x, y, z dương thỏa mãn \(\dfrac{1}{xy}+\dfrac{1}{xz}+\dfrac{1}{yz}=1\)
Chứng minh \(A=\dfrac{x}{\sqrt{yz\left(1+x^2\right)}}+\dfrac{y}{\sqrt{xz\left(1+y^2\right)}}+\dfrac{z}{\sqrt{xy\left(1+z^2\right)}}\le\dfrac{3}{2}\)
Giải:
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow ab+bc+ac=1\)
\(\Rightarrow A=\dfrac{\dfrac{1}{a}}{\sqrt{\dfrac{1}{bc}\left(1+\dfrac{1}{a^2}\right)}}+\dfrac{\dfrac{1}{b}}{\sqrt{\dfrac{1}{ac}\left(1+\dfrac{1}{b^2}\right)}}+\dfrac{\dfrac{1}{a}}{\sqrt{\dfrac{1}{ab}\left(1+\dfrac{1}{c^2}\right)}}\)
\(\Rightarrow A=\sqrt{\dfrac{bc}{a^2+1}}+\sqrt{\dfrac{ac}{b^2+1}}+\sqrt{\dfrac{ab}{c^2+1}}\)
\(\Rightarrow A=\sqrt{\dfrac{bc}{a^2+ab+bc+ac}}+\sqrt{\dfrac{ac}{b^2+ab+bc+ac}}+\sqrt{\dfrac{ab}{c^2+ab+bc+ac}}\)
\(\Rightarrow A=\sqrt{\dfrac{bc}{\left(a+b\right)\left(a+c\right)}}+\sqrt{\dfrac{ac}{\left(a+b\right)\left(b+c\right)}}+\sqrt{\dfrac{ab}{\left(a+c\right)\left(b+c\right)}}\)
\(\Rightarrow A\le\dfrac{1}{2}\left(\dfrac{b}{a+b}+\dfrac{c}{a+c}+\dfrac{a}{a+b}+\dfrac{c}{b+c}+\dfrac{a}{a+c}+\dfrac{b}{b+c}\right)\)
\(\Rightarrow A\le\dfrac{1}{2}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{a+c}{a+c}\right)=\dfrac{3}{2}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{\sqrt{3}}{3}\) hay \(x=y=z=\sqrt{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 2 2019
Đề bài này có rất nhiều vấn đề, đầu tiên không có điều kiện x, y, z gì cả? Dương? Â? Bằng 0? Khác 0?
Sau nữa là chiều của BĐT cũng có vấn đề nốt, mình thử với \(x=y=2;z=\dfrac{4}{3}\) thì vế trái ra \(\dfrac{2+\sqrt{30}}{5}\) mà theo casio cho biết thì số này nhỏ hơn \(\dfrac{3}{2}\) , vậy BĐT cũng sai luôn
29 tháng 9 2023
`@ x+y+z=1`.
`<=>` \(\left\{{}\begin{matrix}x=1-y-z\\y=1-z-x\\z=1-x-y\end{matrix}\right.\)
`P=(x+y)^2/(xy+1-x-y).(y+z)^2/(yz-y-z+1).(x+z)^2/(xy-x-y+1)`.
`<=> ((1-z)^2(1-y)^2(1-x)^2)/((1-x)(1-y)(1-y)(1-z)(1-z)(1-x).`
`=1.`
Vậy `P` không phụ thuộc vào giá trị của biến.
13 tháng 4 2023
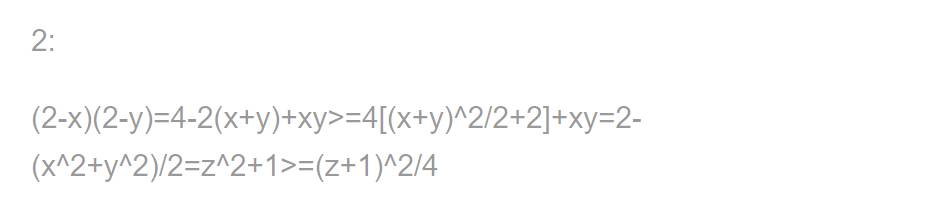
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
AH
Akai Haruma
Giáo viên
19 tháng 3 2018
Lời giải:
Từ \(xy+yz+xz=xyz\Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
Đặt \((a,b,c)=\left(\frac{1}{x}; \frac{1}{y}; \frac{1}{z}\right)\Rightarrow a+b+c=1\)
BĐT cần chứng minh trở thành:
\(P=\frac{c^3}{(a+1)(b+1)}+\frac{a^3}{(b+1)(c+1)}+\frac{b^3}{(c+1)(a+1)}\geq \frac{1}{16}(*)\)
Thật vậy, áp dụng BĐT Cauchy ta có:
\(\frac{c^3}{(a+1)(b+1)}+\frac{a+1}{64}+\frac{b+1}{64}\geq 3\sqrt[3]{\frac{c^3}{64^2}}=\frac{3c}{16}\)
\(\frac{a^3}{(b+1)(c+1)}+\frac{b+1}{64}+\frac{c+1}{64}\geq 3\sqrt[3]{\frac{a^3}{64^2}}=\frac{3a}{16}\)
\(\frac{b^3}{(c+1)(a+1)}+\frac{c+1}{64}+\frac{a+1}{64}\geq 3\sqrt[3]{\frac{b^3}{64^2}}=\frac{3b}{16}\)
Cộng theo vế các BĐT trên và rút gọn :
\(\Rightarrow P+\frac{a+b+c+3}{32}\geq \frac{3(a+b+c)}{16}\)
\(\Leftrightarrow P+\frac{4}{32}\geq \frac{3}{16}\Leftrightarrow P\geq \frac{1}{16}\)
Vậy \((*)\) được chứng minh. Bài toán hoàn tất.
Dấu bằng xảy ra khi \(a=b=c=\frac{1}{3}\Leftrightarrow x=y=z=3\)
21 tháng 11 2017
d)
\(\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+.....+\dfrac{1}{\left(x+99\right)\left(x+100\right)}\)=\(\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+.....-\dfrac{1}{x+99}+\dfrac{1}{x+100}\)=\(\dfrac{1}{x}-\dfrac{1}{x+100}\)
=\(\dfrac{x+100}{x\left(x+100\right)}-\dfrac{x}{x\left(x+100\right)}\)
=\(\dfrac{x+100-x}{x\left(x+100\right)}=\dfrac{100}{x\left(x+100\right)}\)
20 tháng 2 2021
cái chỗ math processing error kia là \(3\left(\dfrac{1}{x^2+1}+\dfrac{1}{y^2+1}+\dfrac{1}{z^2+1}\right)+\left(1+x^2\right)\left(1+y^2\right)\left(1+z^2\right)\ge\dfrac{985}{108}\)
14 tháng 1 2021
Áp dụng bất đẳng thức AM - GM:
\(P\ge3\sqrt[3]{\dfrac{\left(xy+1\right)\left(yz+1\right)\left(zx+1\right)}{xyz}}\).
Áp dụng bất đẳng thức AM - GM ta có:
\(xy+1=xy+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{4}\ge5\sqrt[5]{\dfrac{xy}{4^4}}\).
Tương tự: \(yz+1\ge5\sqrt[5]{\dfrac{yz}{4^4}};zx+1\ge5\sqrt[5]{\dfrac{zx}{4^4}}\).
Do đó \(\left(xy+1\right)\left(yz+1\right)\left(zx+1\right)\ge125\sqrt[5]{\dfrac{\left(xyz\right)^2}{4^{12}}}\)
\(\Rightarrow\dfrac{\left(xy+1\right)\left(yz+1\right)\left(zx+1\right)}{xyz}\ge125\sqrt[5]{\dfrac{1}{4^{12}\left(xyz\right)^3}}\).
Mà \(xyz\le\dfrac{\left(x+y+z\right)^3}{27}=\dfrac{1}{8}\)
Nên \(\dfrac{\left(xy+1\right)\left(yz+1\right)\left(zx+1\right)}{xyz}\ge125\sqrt[5]{\dfrac{8^3}{4^{12}}}=125\sqrt[5]{\dfrac{1}{2^{15}}}=\dfrac{125}{8}\)
\(\Rightarrow P\ge\dfrac{15}{2}\).
Vậy...
HN
17 tháng 1 2021
Áp dụng bất đẳng thức AM - GM:
P≥33√(xy+1)(yz+1)(zx+1)xyz.
Áp dụng bất đẳng thức AM - GM ta có:
xy+1=xy+14+14+14+14≥55√xy44.
Tương tự: yz+1≥55√yz44;zx+1≥55√zx44.
Do đó (xy+1)(yz+1)(zx+1)≥1255√(xyz)2412
⇒(xy+1)(yz+1)(zx+1)xyz≥1255√1412(xyz)3.
Mà xyz≤(x+y+z)327=18
Nên (xy+1)(yz+1)(zx+1)xyz≥1255√83412=1255√1215=1258
⇒P≥152.
\(VT=\dfrac{\left(\dfrac{1}{z}\right)^2}{\dfrac{1}{x}+\dfrac{1}{y}}+\dfrac{\left(\dfrac{1}{x}\right)^2}{\dfrac{1}{y}+\dfrac{1}{z}}+\dfrac{\left(\dfrac{1}{y}\right)^2}{\dfrac{1}{x}+\dfrac{1}{z}}\ge\dfrac{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}{2\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)}=\dfrac{1}{2}\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
Dâu "=" xảy ra khi \(x=y=z\)