Question

[Nguyễn thị Phụng]

Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A ( 4 ; 1) , B ( 10 ; 9 ) , C ( 7 ; -3 )

a) Chứng minh A , B , C không thẳng hàng và tính chu vi của tam giác ABC .

b) Tìm tọa độ điểm D để tứ giác ABDC là hình bình hành .

c) Tính số đo góc A của tam giác ABC .

d) Tìm tọa độ trực tâm và tâm đường tròn ngoại tiếp của tam giác ABC .

e) Tìm tọa độ điểm E là giao điểm của đường thẳng AB với trục Ox .

HELP ME !!!!!!!!!!!!

Answer 1

[Trương Anh]

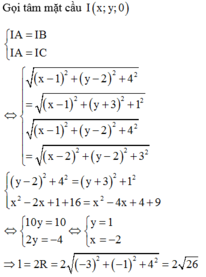
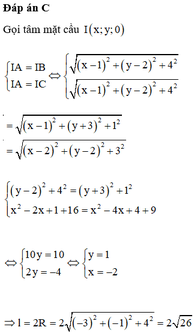
a) Ta có: \(\overrightarrow{AB}=\left(6;8\right)\) ; \(\overrightarrow{AC}=\left(3;-4\right)\) ; \(\overrightarrow{BC}=\left(-3;-12\right)\)

Ta thấy không có vecto nào có cùng tọa độ nên 3 điêm A B C không thẳng hàng

Vẽ lần lượt các đoạn thẳng từ A B C lên Ox và Oy

Ta tính được \(\left|AB\right|=10\) (đv độ dài)

\(\left|AC\right|=5\) (đv độ dài)

\(\left|BC\right|=3\sqrt{17}\) (đv độ dài)

Chu vi \(\Delta\) ABC là: \(15+3\sqrt{17}\) (đv độ dài)

b) Để ABDC là HBH: \(\overrightarrow{AB}=\overrightarrow{CD}\) \(\Leftrightarrow\) \(\left(6;8\right)=\left(x_D-7;y_D+3\right)\)

\(\Leftrightarrow\) \(\hept{\begin{cases}x_D-7=6\\y_D+3=8\end{cases}\Leftrightarrow\hept{\begin{cases}x_D=13\\y_D=5\end{cases}}}\)

c) Vẽ E sao cho \(AE\perp BE\) tại E

H sao cho \(AH\perp CH\) tại H

Xét \(\Delta\) ABE vuông tại E:

\(\sin BAE=\dfrac{BE}{AB}=\dfrac{8}{10}=\dfrac{4}{5}\) \(\Rightarrow\widehat{BAE}\approx57^o\)

Xét \(\Delta\) ACH vuông tại H:

\(\cos CAH=\dfrac{AH}{AC}=\dfrac{3}{5}\) \(\Rightarrow\widehat{CAH}\approx53^o\)

\(\Rightarrow\) \(\widehat{BAC}=53^o+53^o=106^o\)