1. Cho nửa đường tròn (O, R), điểm C nằm trên nửa đường tròn. Kẻ các tiếp tuyến Ax, By tại A và B của nửa đường tròn. OC cắt Ax tại D, đường vuông góc với OC cắt nửa đường tròn tại E, cắt By tại F.
a) Chứng minh: AD. BF không đổi và DF là tiếp tuyến của (O).
b) AE cắt OC tại G, BC cắt OE tại H. Chứng minh: CH. CB = EG. EA và bằng giá trị không đổi.
c) Gọi I là tiếp điểm của DF với (O). IG cắt BC...
Đọc tiếp
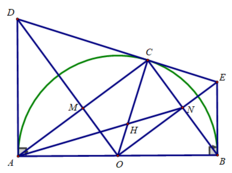
1. Cho nửa đường tròn (O, R), điểm C nằm trên nửa đường tròn. Kẻ các tiếp tuyến Ax, By tại A và B của nửa đường tròn. OC cắt Ax tại D, đường vuông góc với OC cắt nửa đường tròn tại E, cắt By tại F.
a) Chứng minh: AD. BF không đổi và DF là tiếp tuyến của (O).
b) AE cắt OC tại G, BC cắt OE tại H. Chứng minh: CH. CB = EG. EA và bằng giá trị không đổi.
c) Gọi I là tiếp điểm của DF với (O). IG cắt BC tại K, IH cắt AE tại L. Chứng minh: KL // CE và A, K, L, B cùng thuộc một đường tròn (đồng viên)
2. Cho nửa đường tròn (O, R), điểm C chạy trên đường tròn sao cho số đo cung AC không lớn hơn 90o. Kẻ các tiếp tuyến tại A và B của nửa đường tròn. OC cắt tiếp tuyến tại A tại D, đường vuông góc với OC cắt nửa đường tròn tại E, cắt tiếp tuyến tại B tại F. Tiếp tuyến tại C của nửa đường tròn cắt tiếp tuyến tại A tại M, tiếp tuyến tại E của nửa đường tròn cắt tiếp tuyến tại A tại N. AE cắt BC tại J. Chứng minh:
a) DF tiếp xúc với (O) và M, J, N thẳng hàng.
b) Gọi I là tiếp điểm của DF với (O). Chứng minh: MJ. JN \(\le\) DI. IF
c) Tìm quỹ tích của điểm J khi C di động mà thỏa mãn các điều kiện trong giả thiết.
3. Cho nửa đường tròn (O, R), P là điểm chính giữa của cung AB, điểm C chạy trên phần tư đường tròn chứa điểm A (C khác A và P). Kẻ các tiếp tuyến tại A và B của nửa đường tròn. OC cắt tiếp tuyến tại A tại D, đường vuông góc với OC cắt nửa đường tròn tại E, cắt tiếp tuyến tại B tại F.
a) Chứng minh: DF có đúng 1 điểm chung với (O).
b) Gọi I là điểm chung đó, AE cắt BC tại J, AE cắt OC tại G, BC cắt OE tại H. Chứng minh: ICGJ, IEHJ nội tiếp và CE vuông góc với IJ.
c) Gọi K và L là giao của đường tròn ngoại tiếp tứ giác ICGJ, IEHJ với CE. Chứng minh: GL. GI + HK. HI = GC2 + HE2 và tính diện tích lớn nhất của hình ICGJHE theo R.
d) Chứng minh: OG. OC + OH. OE \(\ge\) 2. OJ. OI.
Cần các bạn giúp đỡ, đặc biệt là ý c, d của bài 3 ạ.