cho tam giac ABC.gọi M,N là trung điểm ABvà AC.Trên tia đối củaNM lấy D sao cho NM=ND
a,C/M :AM=DC
b, C/M : MN//CD
c,cm:MD//BC
d, cm MN=1/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2022
a: Xét tứ giác ABCD có
N là trung điểm của AC
N là trung điểm của BD
Do đó: ABCD là hình bình hành
Suy ra: AB//CD
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN=1/2BC
R
25 tháng 1 2022
Tham khảo
a) Xét ΔAMH và ΔNMB có:
+ AM = NM
+ góc AMH = góc NMB (đối đỉnh)
+ MH = MB
=> ΔAMH = ΔNMB (c-g-c)
=> góc MAH = góc MNB
=> AH//BN
Mà AH vuông góc BC
=> BN vuông góc BC
b) Do ΔAMH = ΔNMB
=> AH = BN
Trong tam giác vuông ABH vuông tại H
=> AB > AH (cạnh huyền là cạnh lớn nhất)
=> AB > BN
c) Ta cm được ΔABM = ΔNHM (c-g-c)
=> góc BAM = góc HNM
Trong ΔANH có:NH > AH
=> góc MAH > góc MNH
=> góc MAH > góc BAM
d) Ta cm được ΔABH = ΔACH (ch-cgv)
=> BH = CH
=> CH = 2. HM
Tam giác ANC có CM là đường trung tuyến (do M là trung điểm của AN)
và CH/CM =2/3
=> H là trọng tâm của ΔANC
=> AH là đường trung tuyến
=>AH đi qua trung điểm của CN
hay A,H,I thẳng hàng
4 tháng 1 2022
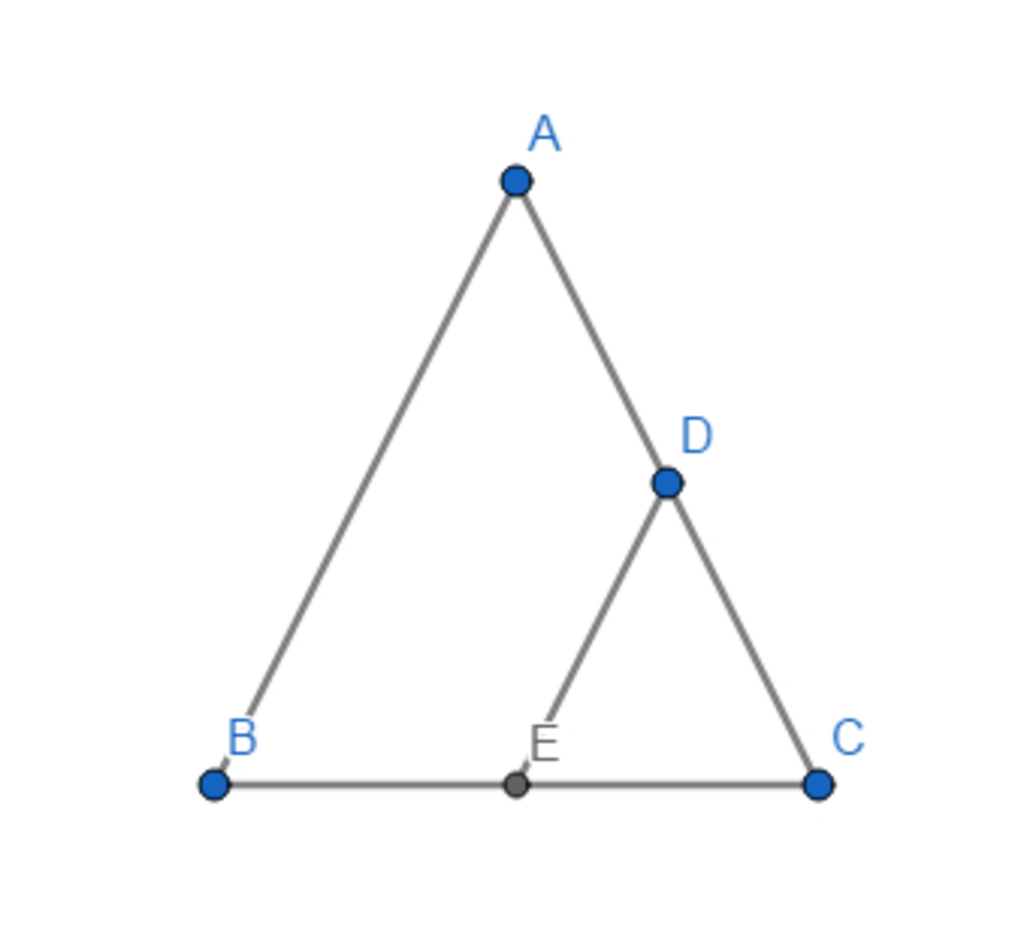
Xét tứ giác AMCD có
N là trung điểm của AC
N là trung điểm của MD
Do đó: AMCD là hình bình hành
Suy ra: CD//AM
hay CD//AB
4 tháng 1 2022
Xét tứ giác AMCD có
N là trung điểm của AC
N là trung điểm của MD
Do đó: AMCD là hình bình hành
Suy ra: CD//AM
hay CD//AB
Chứng minh:
Tam giác ABC có:
M là trung điểm của AB( theo giả thiết)
N là trung điểm của AC( theo giả thiết)
=>MN là đường trung bình của tam giác ABC
=> MN=1/2 BC
Chứng minh định lý:
Trên tia đối của tia NM lấy điểm D sao cho N là trung điểm của MD
Xét tam giác ANM và tam giác CND
Ta có:
AN=NC( theo giả thiết)
Góc ANM=gócCND( hai góc đối đỉnh)
NM=ND(cách vẽ)
Do đó:
Tam giác ANM = tam giác CND( c.g.c)
=> AM=CD( hai cạnh tương ứng)
Và góc A= góc MCD(hai góc tương ứng)
=> AM//CD
=> MB//CD
=> MBCD là hình thang
Lại có:
AM=CD
=> MD=BC và MD//BC
=> MN//BC
Mà N là trung điểm của MD(cách vẽ)
=> MN=1/2 MD
vẽ hình cho mk với