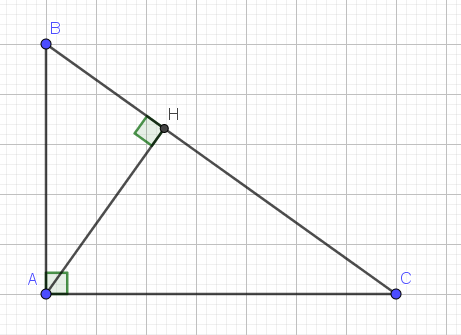
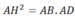cho \(\Delta ABC\) vuông tại A, đường cao AH
1, Biết AB=3cm; BC=5cm. Hãy giải \(\Delta ABC\)
2, Trên tia đối của AH lấy điểm K. Q là hình chiếu của C trên BK, tia AH cắt QC tại I. C/m: \(AH^2\)= HI.HK
3, Lấy M thuộc CQ sao cho BM=AB. Tính số đo góc BMK
HELP MEEEEEEEE!!!!!!!!!!
GIÚP EM ĐI Ạ!!!!!!!!!!