\(5x^2+y^2-4xy+2y+5=0\)
tìm x,y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 9 2021
a) x2+y2-4x+4y+8=0
⇔ (x-2)2+(y+2)2=0
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-2\end{matrix}\right.\)
b)5x2-4xy+y2=0
⇔ x2+(2x-y)2=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
c)x2+2y2+z2-2xy-2y-4z+5=0
⇔ (x-y)2+(y-1)2+(z-2)2=0
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\y-1=0\\z-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\z=2\end{matrix}\right.\)
6 tháng 9 2021
b: Ta có: \(5x^2-4xy+y^2=0\)
\(\Leftrightarrow x^2-\dfrac{4}{5}xy+y^2=0\)
\(\Leftrightarrow x^2-2\cdot x\cdot\dfrac{2}{5}y+\dfrac{4}{25}y^2+\dfrac{21}{25}y^2=0\)
\(\Leftrightarrow\left(x-\dfrac{2}{5}y\right)^2+\dfrac{21}{25}y^2=0\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
DP
1
18 tháng 4 2023
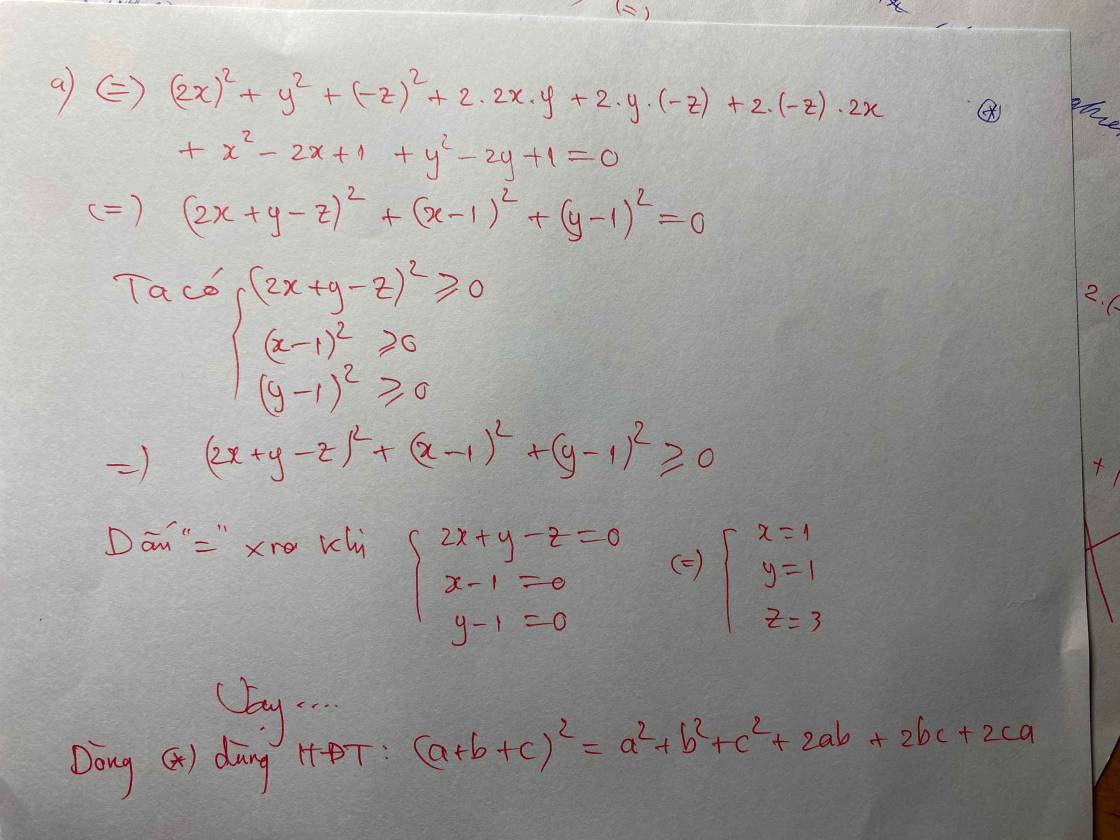
Học tốt nha bn ! ( dòng * ko cần ghi vào đâu bn đây là nháp giở của mik )
N
2
T
29 tháng 5 2016
5x^2+2y^2+4xy-4x-y+5=(4x^2+y^2+4xy)+(x^2-4x+4)+(y^2-y+1/4)+3/4 =(2x+y)^2+(x-2)^2+(y-1/2)^2+3/4 (1)
vi (2x+y)^2>=0 , (x-2)^2>=0 ,(y-1/2)^2>=0 (2)
tu 1 va 2 suy ra dieu phai chung minh
18 tháng 11 2018
a/ \(4x^2+2y^2-4xy+4x-2y+5=0\)
\(\Leftrightarrow\left(4x^2-4xy+y^2\right)+2\left(2x-y\right)+1+4=0\)
\(\Leftrightarrow\left(2x-y\right)^2+2\left(2x-y\right)+1+4=0\)
\(\Leftrightarrow\left(2x-y+1\right)^2+4=0\)
Với mọi x, y ta có :
\(\left(2x-y+1\right)^2\ge0\Leftrightarrow\left(2x-y+1\right)^2+4>0\)
\(\Leftrightarrow pt\) vô nghiệm
TN
2
NC
30 tháng 9 2020
Ta có: \(5x^2-4xy+2x-2y+y^2+2=0\)
\(\Leftrightarrow\left(4x^2-4xy+y^2\right)+\left(4x-2y\right)+1+\left(x^2-2x+1\right)==0\)
\(\Leftrightarrow\left[\left(2x-y\right)^2+2\left(2x-y\right)+1\right]+\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(2x-y+1\right)^2+\left(x-1\right)^2=0\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}\left(2x-y+1\right)^2=0\\\left(x-1\right)^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}\)
NN
6 tháng 12 2017
\(5x^2+6x-4xy-2y+2+y^2=0\)
\(\Leftrightarrow4x^2+x^2+2x+4x-4xy-2y+1+1+y^2=0\)
\(\Leftrightarrow\left(4x^2-4xy+y^2\right)+\left(4x-2y\right)+\left(x^2+2x+1\right)+1=0\)
\(\Leftrightarrow\left(2x-y\right)^2+2\left(2x-y\right)+1+\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(2x-y+1\right)^2+\left(x+1\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-y+1\right)^2=0\\\left(x+1\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-y+1=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2.\left(-1\right)-y+1=0\\x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2-y+1=0\\x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1-y=0\\x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=-1\end{matrix}\right.\)
Vậy \(x=-1\) và \(y=-1\)
NT
2
12 tháng 2 2023
\(3x^2+y^2+4xy=5x+2y+1\)
\(\Leftrightarrow3x^2+x\left(4y-5\right)+\left(y^2-2y-1\right)=0\left(1\right)\)
Coi phương trình (1) là phương trình ẩn x tham số y, ta có:
\(\Delta=\left(4y-5\right)^2-3.4.\left(y^2-2y-1\right)\)
\(=16y^2-40y+25-12y^2+24y+12\)
\(=4y^2-16y+37\)
Để phương trình (1) có nghiệm nguyên thì \(\Delta\) phải là số chính phương hay \(\Delta=4y^2-16y+37=a^2\) (a là số tự nhiên).
\(\Rightarrow4y^2-16y+16+21=a^2\)
\(\Rightarrow a^2-\left(2y-4\right)^2=21\)
\(\Rightarrow\left(a-2y+4\right)\left(a+2y-4\right)=21\)
\(\Rightarrow a-2y+4;a+2y-4\) là các ước số của 21.
Với \(y\ge2\Rightarrow a-2y+4\le a+2y-4\) và \(a+2y-4\ge0\) Lập bảng:
| a-2y+4 | 1 | 3 |
| a+2y-4 | 21 | 7 |
| a | 11 | 5 |
| y | 7 | 3 |
Với \(y\ge2\Rightarrow a-2y+4\le a+2y-4\) và \(a+2y-4\ge0\) Lập bảng:
| a-2y+4 | 21 | 7 |
| a+2y-4 | 1 | 3 |
| a | 11 | 5 |
| y | -3(loại vì y>0) | 1 |
Với a=11, y=7. Phương trình (1) có 2 nghiệm:
\(x_1=\dfrac{-\left(4.7-5\right)+\sqrt{11^2}}{6}=-2\) (loại vì x>0)
\(x_2=\dfrac{-\left(4.7-5\right)-\sqrt{11^2}}{6}=-\dfrac{17}{3}\left(loại\right)\)
Với \(a=5;y=3\). Phương trình (1) có 2 nghiệm:
\(x_1=\dfrac{-\left(4.3-5\right)+\sqrt{5^2}}{6}=-\dfrac{1}{3}\left(loại\right)\)
\(x_2=\dfrac{-\left(4.3-5\right)-\sqrt{5^2}}{6}=-2\) (loại vì x>0)
Với \(a=5;y=1\). Phương trình (1) có 2 nghiệm:
\(x_1=\dfrac{-\left(4.1-5\right)+\sqrt{5^2}}{6}=1\)
\(x_2=\dfrac{-\left(4.1-5\right)-\sqrt{5^2}}{6}=-\dfrac{2}{3}\left(loại\right)\)
Vậy x,y nguyên dương thỏa mãn phương trình trên là \(x=y=1\)
12 tháng 2 2023
cho mình hỏi sao để nó có nghiệm nguyên khi nó là số chính phương thế bạn
\(5x^2+y^2-4xy+2y+5=0\)
\(\Rightarrow\left(4x^2-4xy+y^2\right)-2\left(2x-y\right)+1+x^2+4x+4=0\)
\(\Rightarrow\left(2x-y\right)^2-2\left(2x-y\right)+1+\left(x+2\right)^2=0\)
\(\Rightarrow\left(2x-y-1\right)^2+\left(x+2\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}2x-y-1=0\\x+2=0\end{cases}\Rightarrow}\hept{\begin{cases}y=-5\\x=-2\end{cases}}\)