cho hai hàm số y=2x-4 (d) va y= -x+4 (d')
a, vẽ đồ thị hàm số trên cùng mặt phẳng tọa độ
b,gọi giao điểm của hai đường thẳng (d) vả (d') la Q: xác định tọa độ điểm Q?
c,gọi giao điểm của 2 đường thẳng (d) vả (d') vs trục Oy là M và N. tính diện tích tam giác MNQ?tính các góc của tam giác MNQ ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)
14 tháng 12 2023
a:
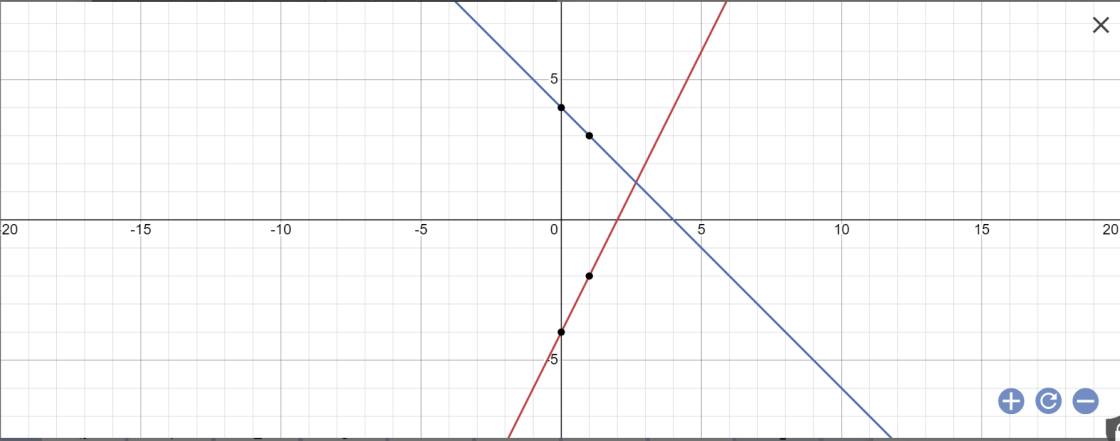
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)
6 tháng 1 2022
a: k=xy=5x2=10
b: Thay x=3 vào y=3x, ta được:
y=3x3=9
Vậy: điểm A(3;9) thuộc đồ thị y=3x
c: f(4)=16-1=15
KC
6 tháng 1 2022
a, Vì 2 đại lượng x và y tỉ lệ nghịch với nhau
⇒ x . y = a (a ≠ 0)
Khi x = 2 thì y = 5
⇒ 2 . 5 = a ⇒ a = 10
Vậy hệ số tỉ lệ của y đối với x là 10
b, x . y = 10 ⇒ y = \(\dfrac{10}{x}\)
c, x . y = 10
x = 5 ⇒ y = 10 : 5 = 2
x = -10 ⇒ y = 10 : (-10) = -1
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
HQ
Hà Quang Minh
Giáo viên
22 tháng 8 2023
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 12 2022
a, Vẽ đồ thị hàm số y = 2x - 4
- Giao đồ thị với trục Ox là điểm có tung độ bằng 0 ; y = 0
=> 2x - 4 = 0 => x = 4/2 => x= 2
Đồ thị cắt trục hành tại A ( 2; 0)
- Giao đồ thị với trục Oy là điểm cs hoành độ bằng 0 ; x = 0
=> y = 0-4 = -4
Đồ thị cắt trục tung tại B ( 0; -4)
Tính khoảng cách từ điểm O đến đt (d) : y = 2x - 4
=> 2x - 4 - y = 0
=> 2x - y - 4 = 0 (d1)
Khoảng cách từ O đến d chính là khoảng cách từ O đến (d1)
Điểm O(0 ;0)
d(0; d1) = \(\dfrac{|2.0-0-4|}{\sqrt{2^2+1^1}}\)
d(O; d1) = \(\dfrac{4}{\sqrt{5}}\) = \(\dfrac{4\sqrt{5}}{5}\)
b, phương trình đt d' có dạng : ax + b
d'//d \(\Leftrightarrow\) a = 2; b # -4
Phương trình đt d' có dạng : 2x + b
Vì d' đi qua A ( 0; 3) nên tọa độ điểm A thỏa mãn pt đường thẳng d.
Thay tọa độ điểm A vào pt đt d' ta có :
2. 0 + b = 3
0 + b = 3
b = 3
vậy các hệ số a; b của đt d' son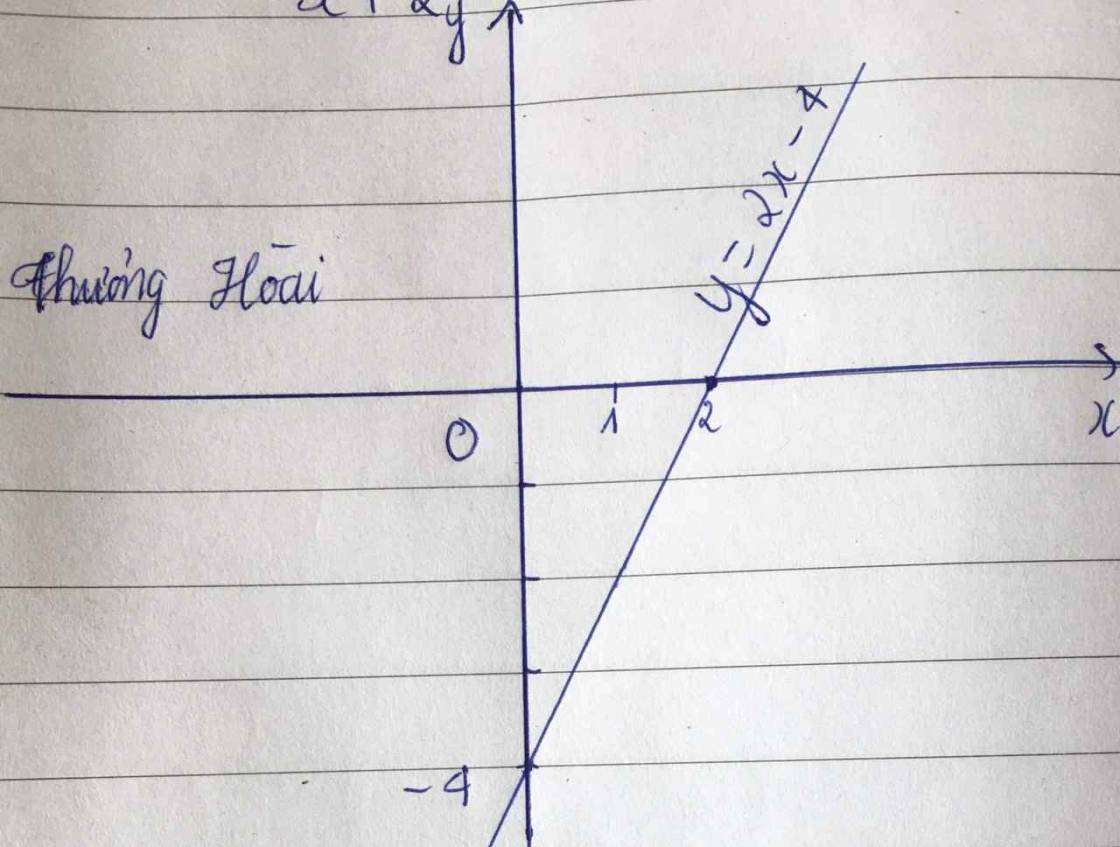
g song với d và đi qua A( 0; 3) lần lượt là : 2; 3
CM
28 tháng 10 2017
Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì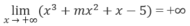 
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
CM
31 tháng 5 2019
Đáp án: D.
Tiệm cận đứng của đồ thị hàm số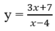 
là x = 4; tiệm cận ngang của đồ thị hàm số đó là y = 3. Diện tích hình chữ nhật tạo thành là 3 x 4 = 12.
14 tháng 8 2023
a: \(y'=4\cdot3x^2-3\cdot2x+2=12x^2-6x+2\)
b: \(y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}=\dfrac{x-1-x-1}{\left(x-1\right)^2}=\dfrac{-2}{\left(x-1\right)^2}\)
c: \(y'=-2\cdot\left(\sqrt{x}\cdot x\right)'\)
\(=-2\cdot\left(\dfrac{x+x}{2\sqrt{x}}\right)=-2\cdot\dfrac{2x}{2\sqrt{x}}=-2\sqrt{x}\)
d: \(y'=\left(3sinx+4cosx-tanx\right)\)'
\(=3cosx-4sinx+\dfrac{1}{cos^2x}\)
e: \(y'=\left(4^x+2e^x\right)'\)
\(=4^x\cdot ln4+2\cdot e^x\)
f: \(y'=\left(x\cdot lnx\right)'=lnx+1\)
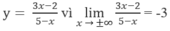
b: Tọa độ Q là:
2x-4=-x+4 và y=2x-4
=>x=8/3 và y=16/3-4=4/3
c: Tọa độ M là:
x=0 và y=2x-4=-4
Tọa độ N là:
x=0và y=-x+4=4
Q(8/3;4/3); M(0;-4); N(0;4)
\(MQ=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
\(C=\left(\dfrac{8\sqrt{5}}{3}+\dfrac{8\sqrt{2}}{3}+8\right)\left(cm\right)\)
Xét ΔMNQ có
\(cosN=\dfrac{NM^2+NQ^2-QM^2}{2\cdot NM\cdot NQ}=\dfrac{\sqrt{2}}{2}\)
nên góc N=45 độ
\(S=\dfrac{1}{2}\cdot NM\cdot NQ\cdot sinN=\dfrac{1}{2}\cdot\dfrac{8\sqrt{2}}{3}\cdot8\cdot\dfrac{\sqrt{2}}{2}=\dfrac{32}{3}\)
\(cosM=\dfrac{MQ^2+MN^2-QN^2}{2\cdot MQ\cdot MN}\)
nên góc M=27 độ
=>góc Q=180-45-27=108 độ