Cho Tam giác abc có góc b - góc c=30 độ tia phân giác bac cắt bc tại d giúp mình nhé ai làm được mình tích cho nhanh lên nhé cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
7 tháng 9 2019
a, B = 2/3 C
=> 3/2 B = C
Xét △ABC, có: A + B + C = 180o
=> 2B + B + 3/2 B = 180o
=> 9/2 B = 180o
=> B = 40o
=> A = 2B = 2 . 40o = 80 180o
=> C = 3/2 B = 3/2 . 40o = 60o
b, Vì BI là phân giác của ABC
=> ABI = IBC = ABC/2 = 40o /2 = 20o
Vì CI là phân giác của ACB
=> ACI = ICB = ACB/2 = 60o /2 = 30o
Xét △BIC có: IBC + BIC + ICB = 180o
=> 20o + BIC + 30o = 180o
=> BIC = 130o
c, Vì AH ⊥ BC => AHB = 90o
Xét △BMH có: MBH + BHM + HMB = 180o
=> 20o + 90o + HMB = 180o
=> HMB = 70o
Ta có: HMB + BMA = 180o (2 góc kề bù)
=> 70o + BMA = 180o
=> BMA = 110o
26 tháng 11 2023
a: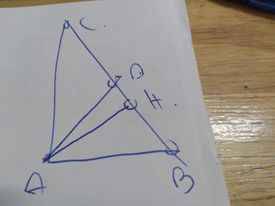 
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot90^0=45^0\)
Xét ΔADC có \(\widehat{ADH}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADH}=\widehat{DAC}+\widehat{DCA}\)
=>\(\widehat{ADH}=45^0+30^0=75^0\)
b: ΔHAD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}+75^0=90^0\)
=>\(\widehat{HAD}=15^0\)
Vì \(\widehat{DAH}< \widehat{DAB}\)
nên AH nằm giữa AD và AB
=>\(\widehat{DAH}+\widehat{BAH}=\widehat{BAD}\)
=>\(\widehat{BAH}+15^0=45^0\)
=>\(\widehat{BAH}=30^0>\widehat{HAD}\)
d: \(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAC}+\widehat{C}=90^0\)(ΔAHC vuông tại H)
Do đó: \(\widehat{ABC}=\widehat{HAC}\)
26 tháng 11 2023
`a)`
`b)`
Có `Delta ABC` vuông tại `A` có `hat(C)=30^0`
`=>hat(B)=60^0`
`AD` là phân giác `hat(BAC)=>hat(BAD)=hat(A_3)=1/2hat(BAC)`
`=>hat(BAD)=hat(A_3)=1/2*90^0=45^0`
`Delta BAD` có `hat(B)+hat(D_1)+hat(BAD)=180^0`
hay `60^0+hat(D_1)+45^0=180^0`
`=>hat(D_1)=180^0-60^0-45^0=75^0`
`c)`
Có `Delta AHD` vuông tại `H(AH⊥BC)` có `hat(D_1)=75^0`
`=>hat(A_1)=15^0`
Có `hat(A_1)+hat(A_2)=hat(BAD)`
hay`15^0+hat(A_2)=45^0`
`=>hat(A_2)=30^0`
Có `15^0<30^0`
`=>hat(A_1)<hat(A_2)`
`d)`
Có `hat(A_1)+hat(A_3)=hat(HAC)`
hay `15^0+45^0=hat(HAC)`
`=>hat(HAC)=60^0`
Có `60^0=60^0`
`=>hat(B)=hat(HAC)`