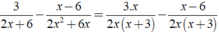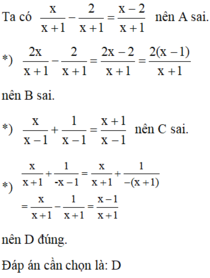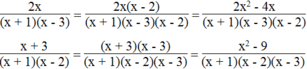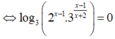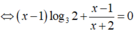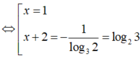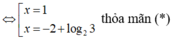1.
Phép tính 32x+6−x−62x2+6x32x+6−x−62x2+6x có kết quả là:
| A. −1x+3−1x+3 | ||
| B. 1x+31x+3 | ||
| C. 1x1x | ||
| D. −1x−1x |
2.
Hiệu của hai phân thức a+9ba2−9b2a+9ba2−9b2 và phân thức 3ba2+3ab3ba2+3ab là phân thức nào sau đây:
| A. 1a1a. | ||
| B. a+3ba(a−3b)a+3ba(a−3b). | ||
| C. −a+3ba(a−3b)−a+3ba(a−3b). | ||
| D. 1a−3b1a−3b. |
3.
Thực hiện phép tính: 3x−64−9x2−13x−2+13x+23x−64−9x2−13x−2+13x+2được kết quả là:
| A. 12x+312x+3 | ||
| B. x−23x+2x−23x+2 | ||
| C. −13x+2−13x+2 | ||
| D. 13x−213x−2 |
4.
Giá trị của biểu thức P=10(x+2)(3−x)−12(3−x)(x+3)−1(x+3)(x+2)P=10(x+2)(3−x)−12(3−x)(x+3)−1(x+3)(x+2)tại x = −34−34 là:
| A. 16451645. | ||
| B. −74−74. | ||
| C. −158−158. | ||
| D. 7474 |
5.
Cho x+4x2−4−1x2+2x=Px+4x2−4−1x2+2x=P thì P bằng phân thức nào sau đây :
| A. x−1x(x−2)x−1x(x−2) | ||
| B. x2−3x−2x(x2−4)x2−3x−2x(x2−4) | ||
| C. x3+3x+2x(x2−4)x3+3x+2x(x2−4) | ||
| D. x+1x(x−2)x+1x(x−2) |
6.
Tổng hai phân thức 1−xx3−11−xx3−1và 1x2−x+11x2−x+1 bằng phân thức nào sau đây:
| A. 2(x−1)x3+12(x−1)x3+1. | ||
| B. 2−xx3+12−xx3+1. | ||
| C. 2+xx3+12+xx3+1. | ||
| D. 2x3+12x3+1 |
7.
Giá trị của biểu thức P=4a2−3a+17a3−1+2a−1a2+a+1+61−aP=4a2−3a+17a3−1+2a−1a2+a+1+61−a tại a = −12−12 là:
| A. - 9 | ||
| B. - 16 | ||
| C. 16 | ||
| D. 9 |
8.
Tổng của các phân thức P: x2+2xy+4y2x2−9y2;x3y−x;y3y+xx2+2xy+4y2x2−9y2;x3y−x;y3y+xbằng phân thức nào sau đây:
| A. x2+y2x2−9y2x2+y2x2−9y2 | ||
| B. y2x2−9y2y2x2−9y2 | ||
| C. (x+y)2x2−9y2(x+y)2x2−9y2 | ||
| D. 0 |
9.
Tổng của các phân thức: x+2y2y2−xy,8xx2−4y2x+2y2y2−xy,8xx2−4y2và 2y−x2y2+xy2y−x2y2+xy là phân thức nào sau đây:
| A. 2(2x−y)x(2y+x)2(2x−y)x(2y+x) | ||
| B. 2(2y−x)y(2y+x)2(2y−x)y(2y+x). | ||
| C. 2y−xy(2y+x)2y−xy(2y+x). | ||
| D. 2(x−2y)y(2y+x)2(x−2y)y(2y+x). |
10.
Tổng của các phân thức ba2−b2,aa2+ab−2a−2bba2−b2,aa2+ab−2a−2b và 1a+b1a+b là:
| A. −2a2−2a+ab(a2−b2)(a−2)−2a2−2a+ab(a2−b2)(a−2). | ||
| B. 2a2−2a+ab(a2−b2)(2−a).2a2−2a+ab(a2−b2)(2−a). | ||
| C. 2a2+2a−ab(a2−b2)(a−2)2a2+2a−ab(a2−b2)(a−2) | ||
| D. 2a2−2a−ab(a2−b2)(a−2)2a2−2a−ab(a2−b2)(a−2). |

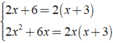 ⇒ MTC = 2x( x + 3 )
⇒ MTC = 2x( x + 3 )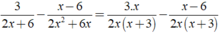
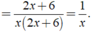
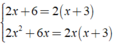 ⇒ MTC = 2x( x + 3 )
⇒ MTC = 2x( x + 3 )