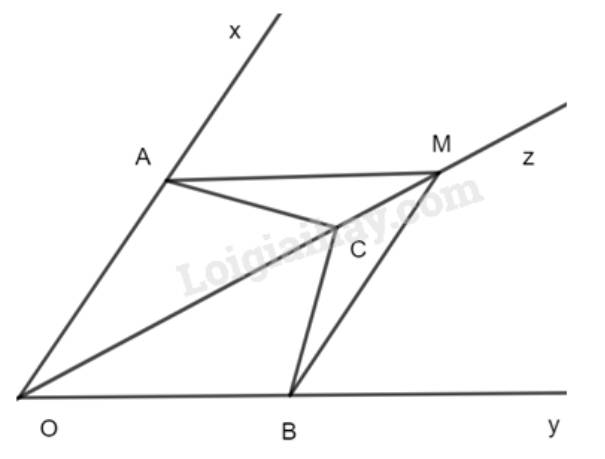
Cho \(\widehat{xOy}\) khác góc bẹt. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Tia phân giác OZ của \(\widehat{xOy}\) cắt AB tại C.
a) Chứng minh \(\Delta\)OAC = \(\Delta\)OBC. Từ đó suy ra OC \(\perp\)AB.
b) Trên tia đối của tia CO lấy điểm D sao cho CD = CO. Chứng minh AD = BO; AB // BO.
c) Gọi M,N lần lượt là trung điểm của AD và OB. Chứng minh 3 điểm M,C,N thẳng hàng.

a: Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đó: ΔOAC=ΔOBC
=>góc OCA=góc OCB=180/2=90 độ
=>OC vuông góc với AB
b: Xét tứ giác OBDA có
C là trug điểm chung của OD và BA
nên OBDA là hình bình hành
=>AD=BO; AD//BO
c: Xét tứ giác BNAM có
BN//AM
BN=AM
Do đó: BNAM là hình bình hành
=>BA cắt NM tại trung điểm của mỗi đường
=>M,C,N thẳng hàng