 giải giúp mình ạ mình ko hiểu cách làm lắm
giải giúp mình ạ mình ko hiểu cách làm lắm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`6x^2+9=0`
Vì \(x^2\ge0\text{ }\forall\text{ x}\)
`\rightarrow`\(6x^2+9\ge9>0\text{ }\forall\text{ x}\)
`\rightarrow` Đa thức vô nghiệm.
Hoặc nếu bạn chưa hiểu hay chưa quen với cách trên thì bạn có thể sử dụng cách này:
\(6x^2+9=0\)
\(\rightarrow\text{ }6x^2=0-9\)
\(\rightarrow\text{ }6x^2=-9\)
Mà \(x^2\ge0\text{ }\forall\text{ x}\)
\(\rightarrow\text{ Đa thức vô nghiệm.}\)
(Cách này mình chỉ giải ra cho bạn hiểu thôi á, còn nếu mà chứng minh thì mình nghĩ cách làm thứ nhất của mình mới dùng dc á cậu).
Dùng phương pháp phản chứng em nhé:
Giả sử đa thức P(\(x\)) = 6\(x^2\) + 9, có nghiệm thì sẽ tồn tại giá trị của \(x\) để:
6\(x^2\) + 9 = 0
Mặt khác ta có: \(x^2\) ≥ 0 ∀ \(x\) ⇒ 6\(x^2\) ≥ 0 ∀ \(x\) ⇒ 6\(x^2\) + 9 > 9 ∀ \(x\)
vậy 6\(x^2\) + 9 = 0 (là sai) hay
Đa thức: 6\(x^2\) + 9 vô nghiệm (đpcm)

Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)

`4xx2,5xx13,251+0,25xx40`
`=4xx2,5xx13,251+0,25xx4xx10`
`=10xx13,251+10`
`=10xx13,251+10xx1`
`=10xx(13,251+1)`
`=10xx14,251`
`=142,51`

1 shall we
2 aren't I
3 isn't there
1 don't they
2 isn't she
3 will they
4 isn't it
5 are there
6 doesn't he
7 wouldn't he
8 are those
9 have you
10 isn't it
11 can't they
12 did they
13 did it
15 aren't I
16 aren't they
17 have you
18 was it
19 hadn't he
20 don't you
21 aren't they
22 have you
23 isn't it
24 are there
25 aren't you
1 didn't you
2 can't we

Chu vi hình tròn là: `157 xx 1,4 = 219,8 (m)`
Bán kính hình tròn là: `291,8 : 3,14 : 2 = 35 (m)`
Diện tích hình tròn là: `35 xx 35 xx 3,14 = 3846,5(m^2)`
Đ/s: `3846,5 m^2`
Chu vi hình tròn:
\(1,4\times157=219,8\left(m\right)\)
Đường kính hình tròn:
\(\dfrac{219,8}{2\times3,14}=35\left(m\right)\)
Diện tích hình tròn:
\(35\times35\times3,14=3846,5\left(m^2\right)\)
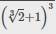 mn giải chi tiết giúp mình bước tách ra được ko ạ tại mình ko hiểu cách tách lắm. cảm ơn mn !
mn giải chi tiết giúp mình bước tách ra được ko ạ tại mình ko hiểu cách tách lắm. cảm ơn mn !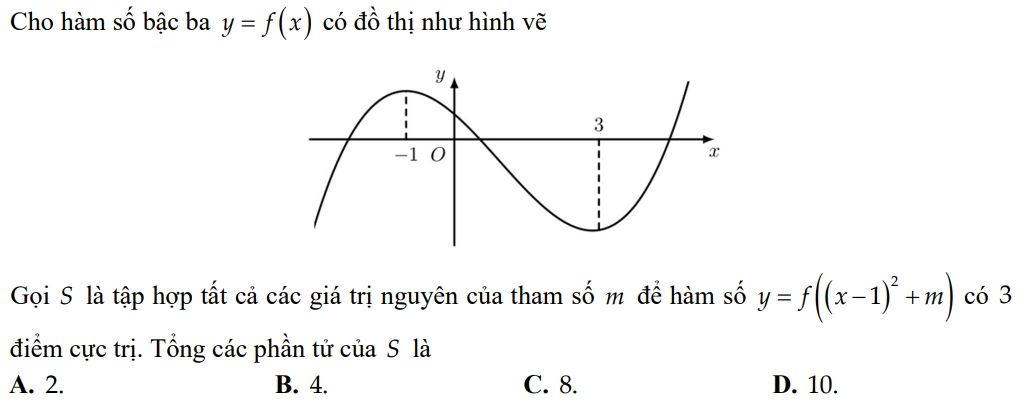
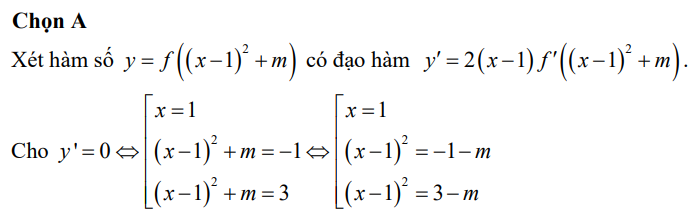
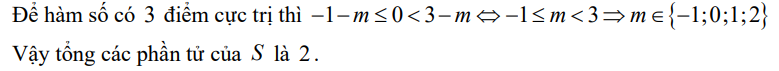



 Làm giúp mình bài này với ạ, mik không hiểu đề lắm ạ.
Làm giúp mình bài này với ạ, mik không hiểu đề lắm ạ. ai hiểu bài này ko giúp mình với sao mà cô ra đề mà mik ko hiểu í bn nào siêng thì làm và chỉ cách giải lun còn nếu ko thì làm bài là đc òi
ai hiểu bài này ko giúp mình với sao mà cô ra đề mà mik ko hiểu í bn nào siêng thì làm và chỉ cách giải lun còn nếu ko thì làm bài là đc òi
a: \(A=\cos^215^0+\cos^225^0+\cos^235^0+...+\cos^255^0+\cos^265^0+\cos^275^0\)
\(=1+1+1+\dfrac{1}{2}\)
\(=\dfrac{7}{2}\)