Tìm giá trị nhỏ nhất của M biết: M= x2 - 6x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
M
3
K
2

18 tháng 12 2021
\(M=x^2-6x+20\\ \Rightarrow M=\left(x^2-6x+9\right)+11\\ \Rightarrow M=\left(x-3\right)^2+11\ge11\)
Dấu "=" xảy ra \(\Leftrightarrow x=3\)
Vậy \(M_{min}=11\Leftrightarrow x=3\)
18 tháng 12 2021
\(M=\left(x-3\right)^2+11>=11\forall x\)
Dấu '=' xảy ra khi x=3
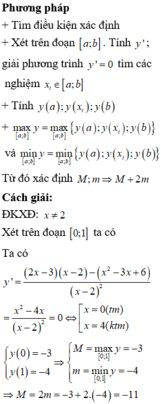
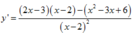
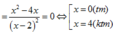
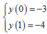
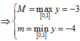

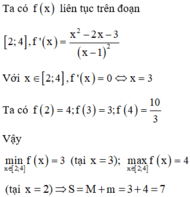
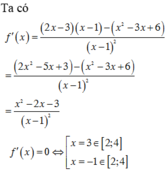
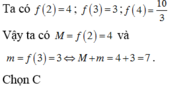
Ta có :
M = x 2 - 6x = x 2 - 6x + 9 - 9 = ( x - 3 ) 2 - 9 \(\ge\)- 9
Dấu ( = ) xảy ra \(\Leftrightarrow\)( x - 3 ) 2 = 0
\(\Leftrightarrow\)x - 3 = 0
\(\Leftrightarrow\)x = 3
Vậy M có giá trị nhỏ nhất = -9 khi x = 3
Ta có:
M=x2-6x=x(x-6)
Amin <=> x(x-6) đạt GTNN
mặt khác: để:Mmin
thì: x>0 vì x=0=> M=0
còn x<0
=> x2-6x E N
Vi Mmin nên x bé nhất có thể
mà: 0<x=> Mmin <=> x=1
Vậy Mmin=1.(-5)=-5