Gọi m là giá trị lớn nhất của hàm số y=3+2sin2x trên đoạn [π/6;π/2].Giá trị m thỏa mãn thức nào dưới đây a.3<m<6 b.m^2=16 c.4<m<5 d.m=3+√3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Ta có: y = 2 s i nx+cos 2 x
= 2 sin x + 1 − 2 sin 2 x → t → s inx y = f x = − 2 t 2 + 2 t + 1.
Với x ∈ 0 ; π ⇒ t ∈ 0 ; 1 .
Xét hàm số f t = − 2 t 2 + 2 t + 1 trên 0 ; 1 có f ' t = − 4 t + 2.
Ta có: f ' t = 0 ⇔ t = 1 2 .
Tính f 0 = 1 ; f 1 2 = 3 2 ; f 1 = 1.
Vậy M = 3 2 m = 1 ⇒ 2 M + m = 4.

\(M=2\cdot\left(1-cos^2x\right)-cosx+1\)
\(=-2\cdot cos^2x-cosx+1\)
\(=-2\cdot\left(cos^2x+\dfrac{1}{2}cosx-\dfrac{1}{2}\right)\)
\(=-2\cdot\left(cos^2x+2\cdot cosx\cdot\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{9}{16}\right)\)
\(=-2\cdot\left(cosx+\dfrac{1}{4}\right)^2+\dfrac{9}{8}\)
-1<=cosx<=1
=>-3/4<=cosx+1/4<=5/4
=>0<=(cosx+1/4)^2<=25/16
=>0>=-2*cos(x+1/4)^2>=-25/8
=>9/8>=-2*cos(x+1/4)^2+9/8>=-25/8+9/8=-16/8=-2
=>M=9/8; m=-2
=>M+m=-7/8

Đáp án C
Phương pháp:
Biến đổi hàm số về hàm số bậc hai đối với cos x , đặt cos x = t và tìm GTLN, GTNN của hàm số với chú ý
Cách giải:
Ta có: y = 2 sin 2 x − cos x + 1
= 2 1 − cos 2 x − cos x + 1 = − 2 cos 2 x − cos x + 3
Đặt t = cos x − 1 ≤ t ≤ 1
y t = − 2 t 2 − t + 3 ⇒ y ' t = − 4 t − 1
y ' 0 = 0 ⇔ t = − 1 4 ∈ − 1 ; 1
⇒ M = max y = y − 1 4 = 25 8 ; m = min y = y 1 = 0 ⇒ M + m = 25 8
Chú ý khi giải:
HS thường nhầm lẫn khi tìm GTLN, GTNN của hàm số, hoặc ở bước đặt ẩn phụ quên không đặt điều kiện cho ẩn mới.

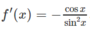
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2
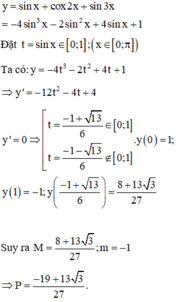
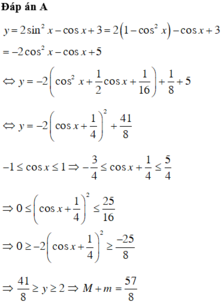
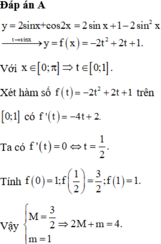
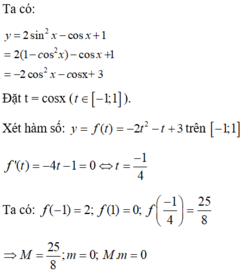
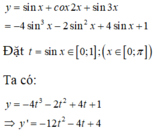
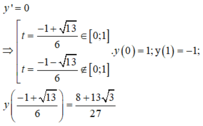

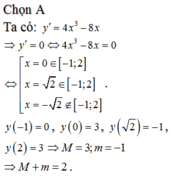
Chọn B