Bài 3 Hai thành phố A, B cách nhau 28km. Cùng một lúc có hai ô tô chạy cùng chiều theo hướng từ A-B, với tốc của ô tô chạy từ A là 54km/h và của ô tô chạy từ B là 40km/h.
a.Lập phương trình chuyển động của mỗi xe?
b.Tìm vị trí mỗi xe sau thời gian 30 phút kể từ lúc khởi hành? Quãng đường mỗi ô tô đi được trong thời gian đó?
c. Xác định tđiểm và vị trí hai xe gặp nhau?
d. Sau bao lâu hai xe cách nhau 42km?
e. Nếu chọn gốc tọa độ tại điểm còn lại thì pt tọa độ của mỗi xe như thế nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

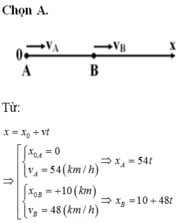
Chọn A
A là mốc → tọa độ ban đầu của 2 xe là x0A = 0 km; x0B = 15 km
Hai xe chuyển động theo chiều dương
→ vA = 40 km/h; vB = 35 km/h
Phương trình chuyển động của vật là x = xo + vt
→ Phương trình chuyển động của ôtô chạy từ A và B lần lượt là
xA = 40t; xB = 15 + 35t

Áp dụng PT chuyển động thẳng đều x = x 0 + vt
Theo dữ kiện của đề bài thì
x 0 A = 0 km, v A = 54 km/h ⇒ PT chuyển động của ô tô chạy từ A là x A = 54t
x 0 B = 10 km, v B = 48 km/h ⇒ PT chuyển động của ô tô chạy từ A là x B = 10 + 48t
Chọn đáp án A
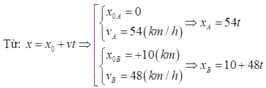




Chiều dương trục Ox : từ A đến B
a,Phương trình chuyển động của mỗi vật:
\(x_1=54t(km,h)\)
\(x_2=28+40t(km,h)\)
b,Đổi 30 phút =0,5 h
Vị trí của mỗi xe cách A sau thời gian 30 phút kể từ lúc khởi hành
\(x_1=54.0,5=27(km)\)
\(x_2=28+40.05=48(km)\)
Quãng đường đi dc của mỗi xe trong thời gian đó
\(s_1=54.0,5=27(km)\)
\(s_2=40.0,5=20(km)\)
c,Khi 2 xe gặp nhau
\(x_1=x_2 \Rightarrow54t= 28+40t\Rightarrow t= 2 (h)\)
Vậy thời điểm 2 xe gặp nhau là sau thời điểm xuất phát 2h
Vị trí gặp cách A :54.2=108(km)
d,hai xe cách nhau 42 km
\(d=\left|x_1-x_2\right|\Rightarrow42=\left|14t-28\right|\Rightarrow\left[{}\begin{matrix}t=5\left(h\right)\left(N\right)\\t=-1\left(h\right)\left(L\right)\end{matrix}\right.\)
Vậy 2 xe cách nhau 42 km sau 5h chuyển động
e, Nếu chọn gốc tọa độ tại B ta có phương trình chuyển động của mỗi xe
\(x_1=-28+54t(km,h)\)
\(x_2=40t(km,h)\)
cam on