Tim a để đa thức x3+x2-x+a chia hết cho x+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

22 tháng 12 2021
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)

22 tháng 12 2021
a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2

29 tháng 10 2021
Bài 1:
Ta có: \(5x^3-3x^2+2x+a⋮x+1\)
\(\Leftrightarrow5x^3+5x^2-8x^2-8x+10x+10+a-10⋮x+1\)
\(\Leftrightarrow a-10=0\)
hay a=10
DL
1

AH
Akai Haruma
Giáo viên
6 tháng 8 2021
Lời giải:
$A(x)=(x^3-x)+(ax^2-a)=x(x^2-1)+a(x^2-1)=(x+a)(x^2-1)$
$=(x+a)B(x)$
Do đó $A(x)$ luôn chia hết cho $B(x)$ với mọi $a$

CM
24 tháng 11 2018
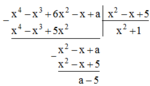
Để có phép chia hết thì số dư phải bằng 0.
Ta có: a – 5 = 0 hay a = 5.

lấy (x3+x2-x+a ):( x+2)=x2-x+1(dư a+2)
để đa thức là phép chia hết
=>a+2=0
=>a=-2
Để \(x^3+x^2-x+a\) chia hết cho x+2 thì với x=-2 thì \(x^3+x^2-x+a\)=0.
Ta có:
\(\left(-2\right)^3+\left(-2\right)^2-\left(-2\right)+a=0\Leftrightarrow-2+a=0\Leftrightarrow a=2\)