Tìm các chữ a và b để so\(\overline{a455}\) chia hết cho3,5 và không chia hết cho 2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
2
AH
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 11 2018
\(\overline{a45b}\) chia hết cho 5 \(\Rightarrow b=0\) hoặc \(b=5\)
Mà \(\overline{a45b}\) không chia hết cho 2 \(\Rightarrow b\) là số lẻ \(\Rightarrow b=5\)
\(\overline{a45b}\) chia hết cho 3 \(\Rightarrow a+4+5+b=a+4+5+5=a+14\) chia hết cho 3
Ta có 14 chia 3 dư 2 \(\Rightarrow a\) chia 3 dư 1
Mà \(1\le a\le9\) \(\Rightarrow a=1;4;7\)
Vậy \(b=5;\) \(a=1\) hoặc \(a=4\) hoặc \(a=7\)
HQ
Hà Quang Minh
Giáo viên
9 tháng 10 2023
a) \(\overline {12x02y} \) chia hết cho 2 và 5 khi chữ số tận cùng của nó là 0.
=> y = 0
\(\overline {12x020} \) chia hết cho 3 khi tổng các chữ số của nó cũng chia hết cho 3.
Nên (1 + 2 + x + 0 + 2 + 0)\( \vdots \)3
=> (x + 5) \( \vdots \) 3 và \(0 \le x \le 9\)
=> x\( \in \) {1; 4; 7}
Vậy để \(\overline {12x02y} \) chia hết cho 2, 3 và cả 5 thì y = 0 và x \( \in \){1; 4; 7}.
b) \(\overline {413x2y} \) chia hết cho 5 mà không chia hết cho 2 khi chữ số tận cùng của nó là 5
=> y = 5
\(\overline {413x25} \)chia hết cho 9 khi tổng các chữ số của nó cũng chia hết cho 9
Nên (4 + 1 + 3 + x + 2 + 5) \( \vdots \)9
=> (x + 15) \( \vdots \)9 và \(0 \le x \le 9\)
=> x = 3.
Vậy \(\overline {413x2y} \) chia hết cho 5 và 9 mà không chia hết cho 2 thì x = 3 và y = 5.
NT
5
5 tháng 12 2016
De 7a2b chia hết cho 5 nhưng không chia hết cho 2 thì b = 5
De 7a25 chia het cho 9 thi 7 + a + 1 + 5 chia het cho 9 hay 13 + a chia het cho 9
=> a = 5
Vậy số tìm được là 7525
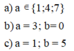
a=1,4,7
b=5