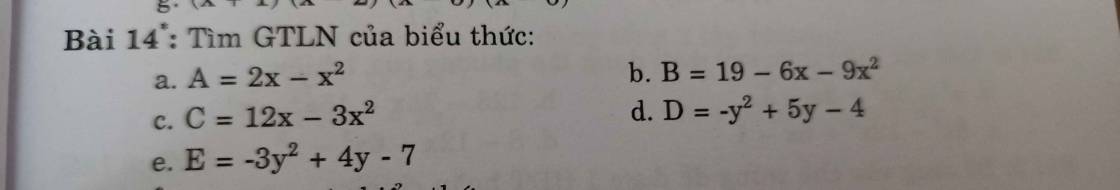Làm giúp 2 câu 24 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(n_{Br_2}=\dfrac{8}{160}=0,05\left(mol\right)\\ C_2H_4+Br_2\rightarrow C_2H_4Br_2\\ n_{C_2H_4}=n_{Br_2}=0,05\left(mol\right)\\ \Rightarrow V_{C_2H_4\left(đktc\right)}=0,05.22,4=1,12\left(l\right)\\ \%V_{\dfrac{C_2H_4}{hh}}=\dfrac{1,12}{3,36}.100\approx33,33\%\\ \Rightarrow\%V_{\dfrac{CH_4}{hh}}=\dfrac{3,36-1,12}{3,36}.100\approx66,67\%\)

1 bỏ so
-In order to V(inf): Để làm gì
3 -So as to V(inf): Để làm gì
6 me->her
-Could/can/Will+V(inf)
-Help+O+V/to V
11 ..... me where the nearest post office is?
-Can/could+S+V+wh-questions+S+V?
14 -Shall+S+V(inf)?
17 ........ going to help him revise his lessons
-"be" going to V(inf): Sẽ làm gì( mang tính chắc chắn)
18 -Would+S+love/like+to V/N?
19 -Let's+V(inf)
= Shall+we+V(inf)?
20 -Trong ngữ cảnh này "to V" được dùng với nghĩa "để làm gì"
*Inf: Infinitive

2 câu tiếp theo :
Em nghe em về quê hương ngay
Em đã sáng tác hết đây này



Lời giải:
a.
$-A=x^2-2x=(x^2-2x+1)-1=(x-1)^2-1\geq 0-1=-1$ (do $(x-1)^2\geq 0$ với mọi $x$)
$\Rightarrow A\leq 1$
Vậy $A_{\max}=1$. Giá trị này đạt tại $x=1$
b.
$-B=9x^2+6x-19=(9x^2+6x+1)-20=(3x+1)^2-20\geq 0-20=-20$
$\Rightarrow B\leq 20$
Vậy $B_{\max}=20$. Giá trị này đạt tại $3x+1=0\Leftrightarrow x=\frac{-1}{3}$
c.
$-C=3x^2-12x=3(x^2-4x)=3(x^2-4x+4)-12=3(x-2)^2-12\geq 3.0-12=-12$
$\Rightarrow C\leq 12$
Vậy $C_{\max}=12$. Giá trị này đạt tại $x-2=0\Leftrightarrow x=2$
d.
$-D=y^2-5y+4=(y^2-5y+2,5^2)-2,25=(y-2,5)^2-2,25\geq -2,25$
$\Rightarrow D\leq 2,25$
Vậy $D_{\max}=2,25$
Giá trị này đạt tại $y-2,5=0\Leftrightarrow y=2,5$
e.
$-E=3y^2-4y+7=3(y^2-\frac{4}{3}y)+7$
$=3[y^2-\frac{4}{3}y+(\frac{2}{3})^2]+\frac{17}{3}=3(y-\frac{2}{3})^2+\frac{17}{3}\geq \frac{17}{3}$
$\Rightarrow E\leq \frac{-17}{3}$
Vậy $E_{\max}=\frac{-17}{3}$ khi $y-\frac{2}{3}=0\Leftrightarrow y=\frac{2}{3}$