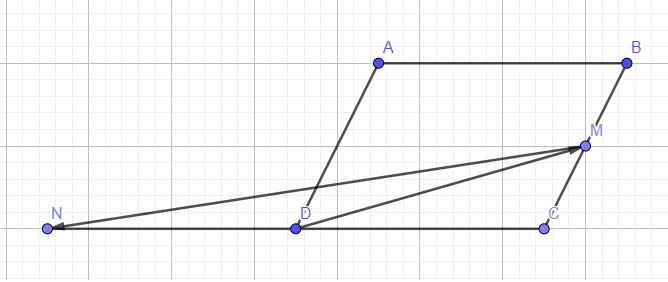
Cho tứ giác ABCD lấy các điểm M,N thỏa mãn vecto AM+2vtBM=vt0 và vecto NC =2/3 vecto DC. CMR vecto MN=2/3AD+1/3BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{NC}=2\overrightarrow{ND}=2\overrightarrow{NC}+2\overrightarrow{CD}\Rightarrow\overrightarrow{NC}=2\overrightarrow{DC}\Rightarrow\overrightarrow{CN}=2\overrightarrow{CD}\)
a.
\(\overrightarrow{DM}=\overrightarrow{DC}+\overrightarrow{CM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{CB}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{CD}=-2\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\\\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MN}=-2\left(\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\right)=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{5}{4}\overrightarrow{BD}\)

\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}=\frac{1}{3}\overrightarrow{AB}+\overrightarrow{BC}+\frac{1}{3}\overrightarrow{CD}\)
\(\Rightarrow\overrightarrow{MN}=\frac{1}{3}\left(\overrightarrow{AD}+\overrightarrow{DC}\right)+\overrightarrow{BC}+\frac{1}{3}\overrightarrow{CD}=\frac{1}{3}\left(\overrightarrow{CD}+\overrightarrow{DC}\right)+\frac{1}{3}\overrightarrow{AD}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{MN}=\frac{1}{3}\overrightarrow{AD}+\overrightarrow{BC}\)
1/3AB thì phải bằng 1/3 (AD+DB) chứ =)) với lại đáp án trắc nghiệm lại không có kết quả này

\(\overrightarrow{NP}=\overrightarrow{NC}+\overrightarrow{CP}\)
\(=\dfrac{2}{3}\overrightarrow{BC}+\dfrac{1}{3}\overrightarrow{CA}\)
\(=-\dfrac{2}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{CA}\)
\(\overrightarrow{PM}=\overrightarrow{PA}+\overrightarrow{AM}\)
\(=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\)
\(=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)\)
\(=\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)

a) \(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\Rightarrow2\overrightarrow{IA}-\overrightarrow{IA}-\overrightarrow{AB}+\overrightarrow{IA}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow2\overrightarrow{AI}=\overrightarrow{AC}-\overrightarrow{AB}\Rightarrow\overrightarrow{AB}+2\overrightarrow{AI}=\overrightarrow{AC}\). Từ đó suy ra cách dựng điểm I:
b) Với cách lấy điểm I như trên, ta có điểm I cố định. Khi đó MN đi qua I, thật vậy:
\(\overrightarrow{MN}=2\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=2\overrightarrow{MI}+2\overrightarrow{IA}-\overrightarrow{MI}-\overrightarrow{IB}+\overrightarrow{MI}+\overrightarrow{IC}\)
\(=2\overrightarrow{MI}+\left(2\overrightarrow{IA}-\overrightarrow{IB}+\overrightarrow{IC}\right)=2\overrightarrow{MI}\)
Suy ra I là trung điểm MN hay MN đi qua điểm I cố định (đpcm).
c) \(\overrightarrow{MP}=\frac{1}{2}\overrightarrow{MB}+\frac{1}{2}\overrightarrow{MN}=\overrightarrow{MA}+\frac{1}{2}\overrightarrow{MC}\)
Đặt K là điểm sao cho \(\overrightarrow{KA}+\frac{1}{2}\overrightarrow{KC}=\overrightarrow{0}\Rightarrow\hept{\begin{cases}K\in\left[AC\right]\\KA=\frac{1}{2}KC\end{cases}}\)tức K xác định
Khi đó \(\overrightarrow{MP}=\overrightarrow{MK}+\overrightarrow{KA}+\frac{1}{2}\overrightarrow{MK}+\frac{1}{2}\overrightarrow{KC}=\frac{3}{2}\overrightarrow{MK}\), suy ra MP đi qua K cố định (đpcm).