Cho tập hợp S = {a1;a2;a3;...a12} gồm 12 phần tử phân biệt. Số các tập con của S có tính chất chỉ số của mỗi phần tử trong tập con là bội của chỉ số nhỏ nhất trong tập đó là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 2 2017
Đáp án C.
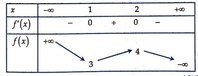
Ta có y ' = 3 x 2 - 12 x + 9 .
Gọi M x 0 ; y 0 là tiếp điểm của tiếp tuyến đi qua A của đồ thị hàm số.
Lúc này tiếp tuyến có phương trình
y = 3 x o 2 - 12 x 0 + 9 x - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
Tiếp tuyến đi qua A 1 ; m ⇒ m = 3 x 0 2 - 12 x 0 + 9 1 - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
⇔ m = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 (*).
Để có đúng một tiếp tuyến của đồ thị hàm số đi qua A thì phương trình (*) có duy nhất một nghiệm.
Xét hàm số f ( x ) = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 có bảng biến thiên
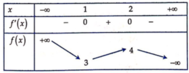
Để phương trình (*) có nghiệm duy nhất thì m > 4 m < 3 ⇔ m ∈ - ∞ ; 3 ∪ 4 ; + ∞ .
Vậy ta chọn C.
CM
30 tháng 7 2018
Đáp án D
Số phần tử của tập 
Để 
chia hết cho 5 điều kiện cần và đủ là 
hay 
Nếu 
thì lấy trong 7 chữ số 1,2,...,7
Vậy có 
số tận cùng bằng 0
Nếu 
thì các số 
là 
số
Vây xác suất để số đó chia hết cho 5 là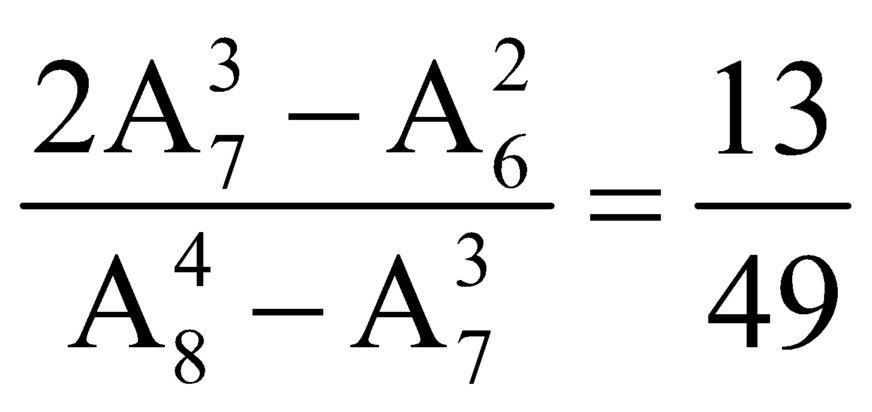 
CM
28 tháng 10 2019
Nối A 1 ∈ E với m điểm B 1 , B 2 , B 3 , . .. , B m ∈ F ta có m đoạn thẳng A 1 B 1 , A 1 B 2 , A 1 B 3 , . .. , A 1 B m . Lần lượt nối A 1 , A 2 , A 3 , . .. , A n ∈ E với m điểm B 1 , B 2 , B 3 , . .. , B m ∈ F ta có số đoạn thẳng có một đầu thuộc E và một đầu thuộc F là m.n đoạn thẳng.
CM
27 tháng 6 2019
a)
7 ∈ A 1 ∉ A e ∈ A A ⊂ B 3 , 7 ⊂ A 1 , 3 , e ⊂ B
b) Tập hợp B gồm có 4 phần tử.
9 tháng 1 2021
a1: A = {57;357;3651}
a2: B = {57;85} ; C = {57;357} ; D = {57;814} ; E = {57;3651} ; G = {85;357} ; H = {85;814} ; L = {85;3651} ; K = {357;814} ; O = {357;3651}
M = {814;3651}
b/ B = {15;20;25;30;35;40;45;50;55;60;65;70;75;80;85;90;95}
Có: (95 - 15) : 5 + 1 = 17 (phần tử)
CM
25 tháng 10 2017
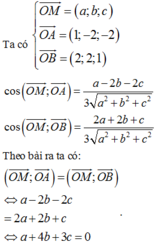
Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán thuộc mặt phẳng x + 4 y + 3 z = 0
Chọn A.