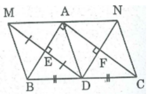
Cho tam giác ABC vuông tại A, trung tuyến AD. Vẽ điểm M ddooid xứng với điểm D qua AB, vẽ điểm N đối xứng với điểm D qua AC. GỌi E và F theo thứ tự là giao điểm của MD và ND với AB và AC.
a) Tứ giác AEDF là hình gì? Vì sao?
b) Các tứ giác ADBM và ADCN là hình gì ? Vì sao?
c) Chứng minh rằng điểm M đối xứng với điểm N qua điểm A.
Giúp mk với mk đang cần rất gấp!

a, ta có
+ M ddooid xứng với điểm D qua AB => md vuông góc vs ab(1)
+ N đối xứng với điểm D qua AC.=>dn vuông góc vs ac(2)
mà tam giác abc vuông tại a(3)
từ 1,2,3 => AEDF là hcn