Tính tổng
S = cos100 + cos300 +...+ cos1500 + cos1700
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 8 2018
Chọn A.
Vì 300 và 600 là hai góc phụ nhau nên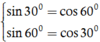 
Suy ra: P = sin300.cos600 + cos300.sin600 = cos600.cos600 + sin600.cos600 = 1.
CM
30 tháng 7 2017
Chọn D.
Vì 300 và 600 là hai góc phụ nhau nên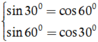 
Do đó: P = cos300.cos600 - sin300.sin600 = cos300.cos600 - cos300.cos600 = 0.
21 tháng 10 2016
Dung kháng của tụ là \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \).
21 tháng 10 2016
Ta có I = 5 A; ${Z_L} = \omega L = 100\pi .0,4 = 40\Omega .$
→ ${U_L} = I{Z_L}$ = 5.40 = 200 V.
HT
4 tháng 12 2019
a/ Khi vật trượt trên mpn
\(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
\(\Rightarrow\left\{{}\begin{matrix}Ox:P.\sin30^0-F_{ms}=m.a\\P.\cos30=N\end{matrix}\right.\)
\(\Rightarrow\frac{1}{2}mg-\mu mg.\frac{\sqrt{3}}{2}=m.a\)
\(\Rightarrow a\approx3\left(m/s^2\right)\)
\(v^2-v_0^2=2aS\Leftrightarrow v=\sqrt{2.3.165}\approx31,5\left(m/s\right)\)
b/\(v^2-v_0^2=2aS\Leftrightarrow-31,5^2=2.a.121\Leftrightarrow a=-4,1\left(m/s^2\right)\)
\(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
\(\Leftrightarrow m.a=-\mu mg\Leftrightarrow-4,1=-10\mu\Leftrightarrow\mu=0,41\)
HY
30 tháng 10 2015
Sử dụng đường tròn
Từ thời điểm 0-0.01 s thì góc quay được là \(\varphi = 0.01.\omega = \pi (rad).\)
I 0 π/3 t=0 M N I 0 2 I 0 2 - t=0.01 P Q t 1 t 2 π/6 φ1 φ2
Thời điểm t =0 ứng với điểm M; thời điểm t = 0.01s ứng với điểm N. Từ M đến N sẽ qua hai điểm P và Q có giá trị (độ lớn) 0.5I0.
tại P: \(\varphi_1 = t_1 \omega => t_1 = \frac{\pi/3}{100\pi} = \frac{1}{300}s\)
tại Q: \(\varphi_2 = t_2 \omega => t_2 = \frac{\pi/3+\pi/6+\pi/6}{100\pi} = \frac{2}{300}s\)
chọn đáp án. A
VT
17 tháng 6 2017
Ta vẽ giản đồ vectơ : U → = U A M → + U M N → + U N B →
Trong đó U A M → ↑ ↑ I → ; U N B → ⊥ I →
Hai tam giác ABM và NBM bằng nhau (có các cạnh lần lượt bằng nhau) dẫn tới kết quả hai tam giác vuông HAB và HNM đồng dạng, suy ra
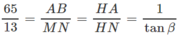
⇒ tan β = 16/65 = 1/5
Trên Hình 15.1.G
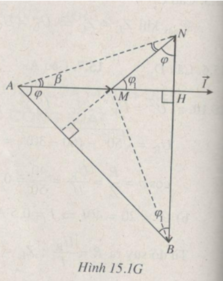
2 β = φ 1
⇒ sin φ 1 = sin2 β
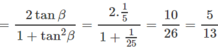
Mặt khác theo Hình 15.1G, ta có :
φ + φ1 = π/2 ⇒ cosφ = sinφ1 = 5/13
30 tháng 9 2016
\(\Delta\varphi=\omega\frac{x_2-x_1}{v}=5\pi\)
hai giao động ngược pha
S= (cos100+cos1700) + (cos300+cos1500) + (cos500+cos1300)+(cos700+1100)+cos900
=0