Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Do ΔABC cân tại A
=> AB = AC; góc ABC=góc ACB
Lại có: góc ABC+ góc ABD = 180o (kề bù)
góc ACB + góc ACE = 180o (kề bù)
=> góc ABD = góc ACE
Xét ΔADB và ΔAEC có:
góc BAD = góc CAE (gt)
AB = AC (cmt)
góc ABD = góc ACE (cmt)
=> ΔADB = ΔAEC (g.c.g)
=> BD = CE (2 cạnh tg ứng) đpcm
b) Vì ΔADB = ΔAEC (câu a)
=> góc ADB = góc AEC (2 góc t/ư)
hay góc HDB = góc KEC
Xét ΔBHD vuông tại H và ΔCKE vuông tại E có:
BD = CE (câu a)
góc HDB = góc KEC(cmt)
=> ΔBHD = ΔCKE (ch - gn)
=> BH = CK (2 cạnh tg ứng) (đpcm)
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\) và AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
c: Xét ΔADE có AH/AD=AK/AE
DO đó: HK//DE
hay BC//HK
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)
Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)
∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)
Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE
+) Xét ΔABD và ΔACE có:
∠DAB = ∠EAC ( giả thiết)
AB = AC (vì tam giác ABC cân tại A)
∠ABD = ∠ACE ( chứng minh trên )
⇒ ΔABD = ΔACE (g.c.g)
⇒ BD = CE ( hai cạnh tương ứng)..
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
c: Xét ΔADE có
AH/AD=AK/AE
nên HK//DE
hay HK//BC
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
c: Xét ΔABC có AH/AD=AK/AE
nên KH//DE
=>KH//CB
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
a) Xét \(\Delta ADB\) và \(\Delta AEC\) có:
\(AB=AC\) (do \(\Delta ABC\) cân tại \(A\))
\(\widehat{ABD}=\widehat{ACE}\)
\(BD=CE\) (giả thiết)
\(\Rightarrow\Delta ADB=\Delta AEC\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) (\(2\) cạnh tương ứng)
\(\Rightarrow\Delta ADE\) cân tại \(A\)
b) Vì \(\Delta ADE\) cân tại \(A\)
\(\Rightarrow\widehat{ADB}=\widehat{ACE}\) (\(2\) góc tương ứng)
Ta có: \(\left\{{}\begin{matrix}\widehat{ADB}+\widehat{HBD}=90^o\\\widehat{ACE}+\widehat{KCE}=90^o\end{matrix}\right.\) (\(2\) góc phụ nhau)
Từ hai điều trên \(\Rightarrow\widehat{HBD}=\widehat{KCE}\)
Mà \(\left\{{}\begin{matrix}\widehat{HBD}=\widehat{CBI}\\\widehat{KCE}=\widehat{BCI}\end{matrix}\right.\) (\(2\) góc đối đỉnh)
Từ đó \(\Rightarrow\widehat{CBI}=\widehat{BCI}\)
\(\Rightarrow\Delta BIC\) cân tại \(I\)
c) Xét \(\Delta ABI\) và \(\Delta ACI\) có:
\(AB=AC\) (giả thiết)
\(BI=CI\) (do \(\Delta BIC\) cân tại \(I\))
\(AI\) là cạnh chung
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\Rightarrow\widehat{AIB}=\widehat{AIC}\) (\(2\) góc tương ứng)
\(\Rightarrow AI\) là tia phân giác \(\widehat{BIC}\)
Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)
Ta có: ∠(ABC) +∠(ABD) =180o(hai góc kề bù)
∠(ACB) +∠(ACE) =180o(hai góc kề bù)
Suy ra: ∠(ABD) =∠(ACE)
Xét ΔABD và ΔACE, ta có:
AB = AC (gt)
∠(ABD) =∠(ACE) (chứng minh trên)
BD=CE (gt)
Suy ra: ΔABD= ΔACE (c.g.c)
⇒∠D =∠E (hai góc tương ứng)
Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:
∠(BHD) =∠(CKE) = 90º
BD=CE (gt)
∠D =∠E (chứng minh trên)
Suy ra: ΔBHD= ΔCKE (cạnh huyền – góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
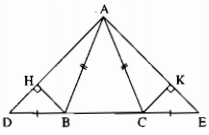
Hình tự vẽ nha
a) Vì tam giác ABC cân tại A
=> ABC = ACB (1)
Ta có ABC + ABD = ACB + ACE ( cùng = 1800 ) (2)
Từ (1) và (2) => ABD = ACE
Xét tam giác ABD và tam giác ACE có :
AB = AC ( gt )
ABD = ACE ( cmt )
BD = CE ( gt )
=> tam giác ABD = tam giác ACE ( c-g-c )
=> D = E
Xét tam giác BHD và tam giác CKE có :
DHB = EKC ( = 900 )
BD = CE ( gt )
D = E ( cmt )
=> tam giác BHD = tam giác CKE ( ch - gn )
=> đpcm
b) Vì tam giác ABD = tam giác ACE ( chứng minh câu a )
=> HAB = KAC ( 2 góc tương ứng )
Xét tam giác AHB và tam giác AKC có :
HAB = KAC ( cmt )
AHB = AKC ( = 900 )
AB = AC ( gt )
=> tam giác AHB = tam giác AKC ( ch - gn )
=> đpcm
c) Nối H với K
Xét tam giác ADE cân tại A ( vì AD = AE )
=> \(\widehat{D}=\frac{180^0-\widehat{DAE}}{2}\left(1\right)\)
Xét tam giác AHK cân tại A ( vì AH = AK )
\(\Rightarrow\widehat{AHK}=\frac{180^0-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) => D = AHK
mà 1 góc này ở vị trí đồng vị
=> HK // DE hay HK // BC ( đpcm )
Có j lên đây hỏi nha : Group Toán Học