Mn ơi giúp em vs ạ em cảm ơn nhìu ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
0
16 tháng 1 2024
a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB
15 tháng 12 2023
Bài 3:
b: Gọi K là giao điểm của AB và OP
Xét (O) có
PA,PB là các tiếp tuyến
Do đó: PA=PB
=>P nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra PO là đường trung trực của AB
=>PO\(\perp\)AB tại K và K là trung điểm của AB
Ta có: ΔOAP vuông tại A
=>\(AP^2+AO^2=OP^2\)
=>\(AP^2=OP^2-OA^2=d^2-R^2\)
=>\(AP=\sqrt{d^2-R^2}\)
Xét ΔOAP vuông tại A có AK là đường cao
nên \(AK\cdot OP=AO\cdot AP\)
=>\(AK\cdot d=R\cdot\sqrt{d^2-R^2}\)
=>\(AK=\dfrac{R\cdot\sqrt{d^2-R^2}}{d}\)
K là trung điểm của AB
=>\(AB=2\cdot AK=\dfrac{2\cdot R\cdot\sqrt{d^2-R^2}}{d}\)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(BA^2+AC^2=BC^2\)
=>\(AC^2=\left(2R\right)^2-\left(\dfrac{2R\sqrt{d^2-R^2}}{d}\right)^2\)
=>\(AC^2=4R^2-\dfrac{4R^2\cdot\left(d^2-R^2\right)}{d^2}\)
=>\(AC^2=\dfrac{4R^2d^2-4R^2\left(d^2-R^2\right)}{d^2}=\dfrac{4R^4}{d^2}\)
=>\(AC=\dfrac{2R^2}{d}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AC\cdot AB\)
=>\(AH\cdot2R=\dfrac{2R^2}{d}\cdot\dfrac{2R\sqrt{d^2-R^2}}{d}\)
=>\(AH=\dfrac{R\cdot2R\sqrt{d^2-R^2}}{d^2}=\dfrac{2R^2\cdot\sqrt{d^2-R^2}}{d^2}\)
KT
1
KN
14
4 tháng 4 2019
Trả lời : Tk mk trước đi .
Hok_Tốt
#Thiên_Hy
DN
1
YP
8 tháng 11 2022
EX1:
1. A
2.A
3.A
4.D
5.D
6.A
7.C
8.B
9.B
10.C
11.B
EX2:
1. Tired
2. gives her
3. lot of
4.much does
5. as expensive as
LV
1
TM
4 tháng 11 2023
a, xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có \(AM\) là đường cao
\(BC^2=AB^2+AC^2\left(pytago\right)\Leftrightarrow BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
\(sinABC=\dfrac{AC}{BC}=\dfrac{16}{20}\Rightarrow\widehat{ABC}\approx53^o8'\)
\(sinACB=\dfrac{AB}{BC}=\dfrac{12}{20}\Rightarrow\widehat{ACB}\approx32^o52'\)
\(AB^2=BM.BC\Rightarrow BM=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7,2\left(cm\right)\)
b, Xét \(\Delta ABM\left(\widehat{AMB}=90^o\right)\) có \(AE\perp AB\)
\(AB^2=BM^2+AM^2\left(pytago\right)\Leftrightarrow AM=\sqrt{20^2-7,2^2}=\dfrac{16\sqrt{34}}{5}\left(cm\right)\)
\(AM^2=AE.AB\) (hệ thức lượng trong tam giác vuông)\(\left(1\right)\)
c, Xét \(\Delta AMC\left(\widehat{AMC}=90^o\right)\)
\(AC^2=AM^2+MC^2\left(pytago\right)\Leftrightarrow AM^2=AC^2-MC^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow AE.AB=AC^2-MC^2\left(đpcm\right)\)
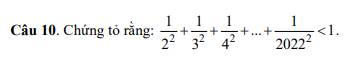
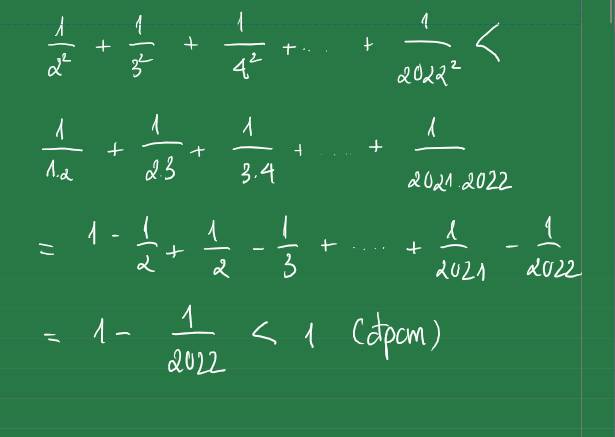
Bài 1: \(n_{CuO}=\dfrac{3,2}{80}=0,04\left(mol\right)\)
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
0,04 → 0,04
\(\Rightarrow m_{H_2SO_4}=0,04\cdot98=3,92\left(g\right)\)
\(\Rightarrow C\%_{H_2SO_4}=\dfrac{3,92}{80}\cdot100\%=4,9\%\)
Bài 2: \(n_{HCl}=0,2\cdot2=0,4\left(mol\right)\)
\(Fe_2O_3+6HCl\rightarrow2FeCl_3+3H_2\uparrow\)
\(\dfrac{1}{15}\) ← 0,4
\(\Rightarrow m_{Fe_2O_3}=\dfrac{1}{15}\cdot160=\dfrac{32}{3}\left(g\right)\)