Vẽ đồ thị hàm số y= 3 - √x²-4x+4
* x²-4x+4 trong căn ạ
* Mn giúp em mai em phải trả bài 😢
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y=\left|x+1\right|+\sqrt{\left(x-2\right)^2}=\left|x+1\right|+\left|x-2\right|\)
\(\Rightarrow\left\{{}\begin{matrix}y=2x-1\text{ với }x\ge2\\y=1-2x\text{ với }x\le-1\\y=3\text{ với }-1\le x\le2\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau (vẽ 3 đồ thị hàm bậc nhất xác định trên trên ở từng khoảng của chúng)
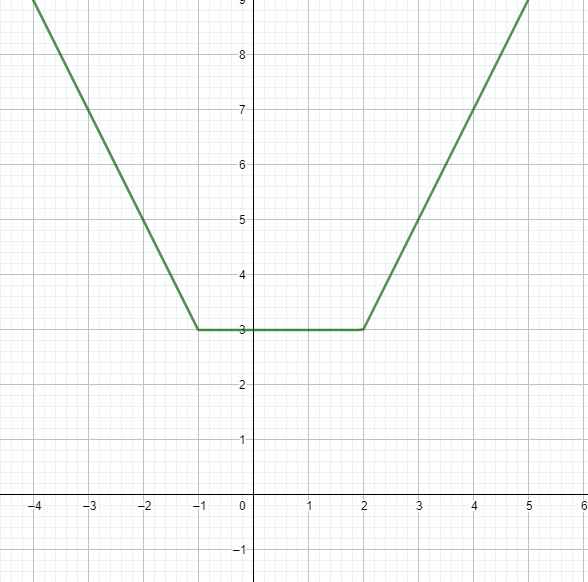
Từ đồ thị \(\Rightarrow y_{min}=3\) khi \(-1\le x\le2\)

Bài 3:
\(A=\dfrac{2\sqrt{x}-4}{3\sqrt{x}-4}+\dfrac{x+22\sqrt{x}-32}{3x-10\sqrt{x}+8}+\dfrac{4+2\sqrt{x}}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}-4}{3\sqrt{x}-4}+\dfrac{x+22\sqrt{x}-32}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}+\dfrac{2\sqrt{x}+4}{\sqrt{x}-2}\)
\(=\dfrac{\left(2\sqrt{x}-4\right)\left(\sqrt{x}-2\right)+x+22\sqrt{x}-32+\left(2\sqrt{x}+4\right)\left(3\sqrt{x}-4\right)}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2x-8\sqrt{x}+8+x+22\sqrt{x}-32+6x-8\sqrt{x}+12\sqrt{x}-16}{\left(3\sqrt{x}-4\right)\cdot\left(\sqrt{x}-2\right)}\)
\(=\dfrac{9x+18\sqrt{x}-40}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{9x-12\sqrt{x}+30\sqrt{x}-40}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(3\sqrt{x}-4\right)\left(3\sqrt{x}+10\right)}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}+10}{\sqrt{x}-2}\)
Bài 2:
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+\dfrac{3}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\3-x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
=>A(3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{2}x+\dfrac{3}{2}=-\dfrac{1}{2}\cdot0+\dfrac{3}{2}=1,5\end{matrix}\right.\)
=>B(0;1,5)
\(OA=\sqrt{\left(3-0\right)^2+\left(0-0\right)^2}=\sqrt{3^2+0^2}=3\)
\(OB=\sqrt{\left(0-0\right)^2+\left(1,5-0\right)^2}=1,5\)
Ox\(\perp\)Oy nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=2.25\)
Bài 1:
a: ĐKXĐ: \(x\in R\)
\(\sqrt{x^2+4x+4}=2\)
=>\(\sqrt{\left(x+2\right)^2}=2\)
=>|x+2|=2
=>\(\left[{}\begin{matrix}x+2=2\\x+2=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b: ĐKXĐ: x>=2
\(\sqrt{4x-8}-7\cdot\sqrt{\dfrac{x-2}{49}}=5\)
=>\(2\sqrt{x-2}-7\cdot\dfrac{\sqrt{x-2}}{7}=5\)
=>\(\sqrt{x-2}=5\)
=>x-2=25
=>x=27(nhận)

a)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=-x^2+4x-3 vào vùng nhập lệnh như hình bên
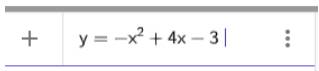
Ta có ngay parabol trên vùng làm việc như hình dưới:
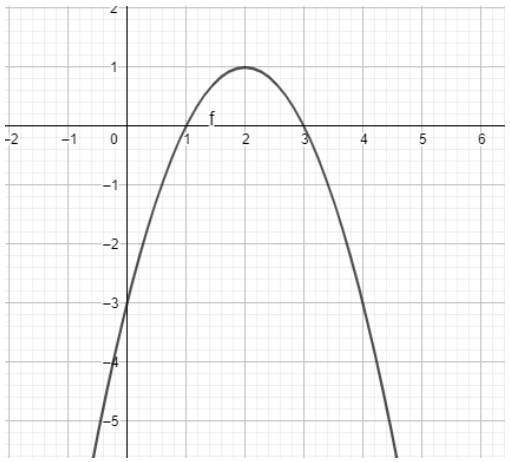
b)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2+2 vào vùng nhập lệnh như hình bên
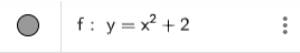
Ta có ngay parabol trên vùng làm việc như hình dưới:
c)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
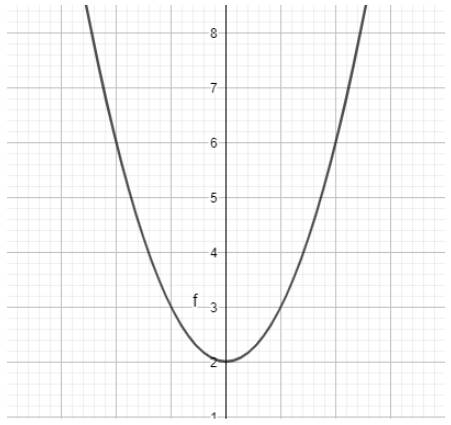
2. Nhập phương trình bậc hai theo cú pháp y=1/2x^2+x+1 vào vùng nhập lệnh như hình bên
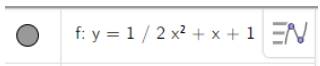
Ta có ngay parabol trên vùng làm việc như hình dưới:
d)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
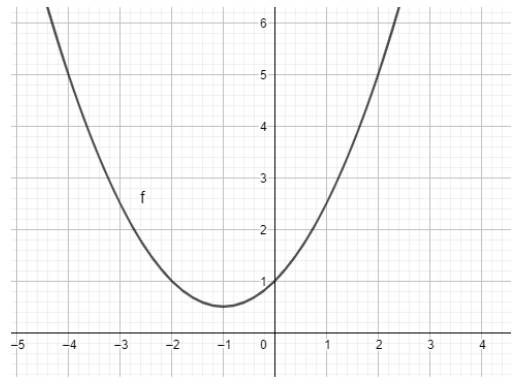
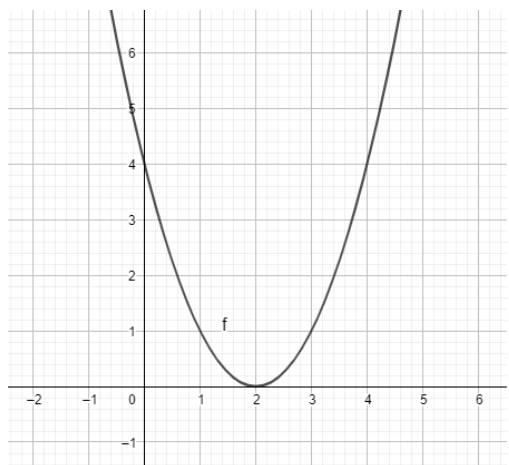
2. Nhập phương trình bậc hai theo cú pháp y=x^2-4x+4 vào vùng nhập lệnh như hình bên
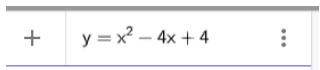
Ta có ngay parabol trên vùng làm việc như hình dưới:

\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
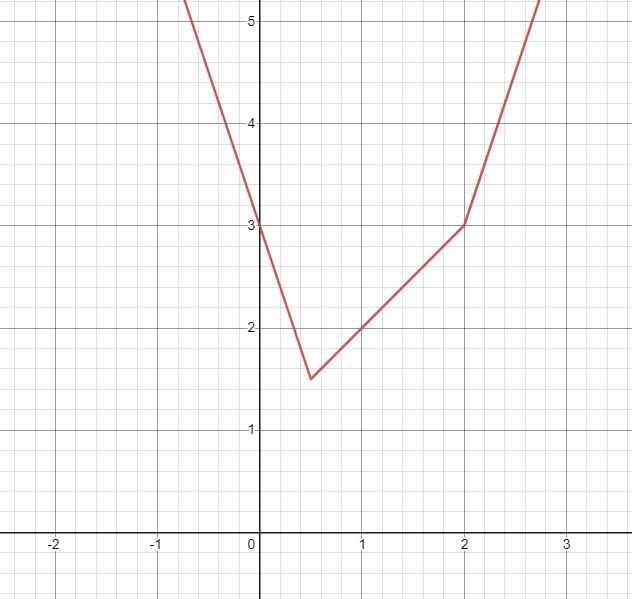
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)