Tìm a,b để đa thức f(x)=x4+ax+b chia hết cho x2-4
HELP ME!!!!!!!!!!!!!!!!!
Mình tính ra a=0, b=4, mn coi đúng không???
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(x\right)⋮g\left(x\right)\)
\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)
\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)

Ta có

Phần dư của phép chia f(x) cho g(x) là R = (a – 1)x + b + 30
Để phép chia trên là phép chia hết thì R = 0 với mọi x
ó (a – 1)x + b + 30 = 0 với mọi x
ó a - 1 = 0 b + 30 = 0 ó a = 1 b = - 30
Vậy a = 1; b = -30
Đáp án cần chọn là: D

Đặt phép chia sau đo tính số dư
Vì x4+1 chia hết cho x2+ax +b ∀ x
⇒ số dư = 0 ⇒ từng cái = 0 ⇒ a= ; b =

Ta có
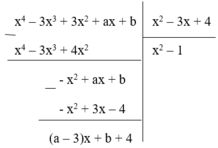
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A

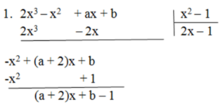
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1

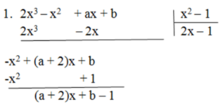
A(x) chia hết cho B(x) khi (a + 2)x + b – 1 là đa thức 0
Vậy a + 2 = 0 và b – 1 = 0 ⇒ a = -2 và b = 1
Gọi thương khi chia f(x) cho x^2-4 là Q(x), ta có;
x^4+ax+b=(x+2)(x-2).Q(x)
Vì đẳng thức đúng với mọi x nên lần lượt cho x=-2,x=2 ta được:
<=> 16−2a+b=0 và 16+2a+b=0
<=> -2a+b=-16 và 2a+b=-16
<=> a=0 và b=-16
Vậy với a=0;b=-16 thì f(x) chia hết cho \(x^2\)- 4
Thực hiện phép chia \(x^4+ax+b\div x^2-4\)ta được số dư là ax + b + 16
Để \(x^4+ax+b⋮x^2-4\)=> ax + b + 16 \(⋮x^2-4\)
=> \(\hept{\begin{cases}ax=0\\b+16=0\end{cases}\Rightarrow\hept{\begin{cases}a=0\\b=-16\end{cases}}}\)