Bài 3 giải sao vậy ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
\(2-2cos^22x=cos2x+1\)
\(\Leftrightarrow2cos^22x+cos2x-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=1\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)
NN
1
HT
12 tháng 12 2020
a/ \(F_{ms}=F_k\Leftrightarrow\mu mg=F_k=0,2.2.10=4\left(N\right)\)
b/ \(F_{ms}=-ma\Leftrightarrow a=-\dfrac{F_{ms}}{m}=-\mu g=-0,2.10=-2\left(m/s^2\right)\)
\(S=v_0t+\dfrac{1}{2}at^2=v_0t-t^2\)
Nếu đề bài ko sai thì v0=0 (m/s) thì thời gian đi hết bằng 0 sẽ nhỏ nhất thôi, bởi vì nhìn cái hàm kia là biết có 3 đại lượng S,v0 và t luôn liên hệ với nhau, thay đổi v0 thì sẽ dẫn đến thay đổi t (nếu coi S là const), nên tui nghĩ chỉ có thể là bằng 0 thôi. Bạn thử lên xem giáo viên nói thế nào đi về cta bàn tiếp
T
1
Y
31 tháng 5 2023
Mình giải thích từ dấu tương đương 2 nha.
\(\dfrac{2x\left(x-2\right)+2x}{2x\left(x-1\right)\left(x-2\right)}=\dfrac{3\left(x-1\right)\left(x-2\right)}{2x\left(x-1\right)\left(x-2\right)}\)
\(\Leftrightarrow\dfrac{2x^2-4x+2x}{2x\left(x-1\right)\left(x-2\right)}-\dfrac{3\left(x-1\right)\left(x-2\right)}{2x\left(x-1\right)\left(x-2\right)}=0\)
\(\Leftrightarrow\dfrac{2x^2-2x-3\left(x^2-2x-x+2\right)}{2x\left(x-1\right)\left(x-2\right)}=0\)
Tới đây phải khử mẫu pt bằng cách lấy mẫu \(2x\left(x-1\right)\left(x-2\right)\) nhân với 0 bên vế phải thì pt mới đơn giản để giải tiếp được.
\(\Leftrightarrow2x^2-2x-3x^2+6x+3x-6=0\)
\(\Leftrightarrow2x^2-2x=3x^2-9x+6\)
Tới đây là ra được dấu tương đương 3 rồi đó.
17 tháng 3 2022
bạn bấm máy tính hoặc giải hệ:
\(\left\{{}\begin{matrix}27x+56y=11\\1,5x+y=0,4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}27x+56y=11\\84x+56y=22,4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}57x=11,4\\27x+56y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0,2\\27.0,2+56y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0,2\\y=0,1\end{matrix}\right.\)
L
1
30 tháng 11 2023
ĐKXĐ: \(5x^2+2x-3>=0\)
=>\(5x^2+5x-3x-3>=0\)
=>\(\left(x+1\right)\left(5x-3\right)>=0\)
TH1: \(\left\{{}\begin{matrix}x+1>=0\\5x-3>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-1\\x>=\dfrac{3}{5}\end{matrix}\right.\)
=>\(x>=\dfrac{3}{5}\)
TH2: \(\left\{{}\begin{matrix}x+1< =0\\5x-3< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =-1\\x< =\dfrac{3}{5}\end{matrix}\right.\)
=>\(x< =-1\)
\(\left(x+1\right)\cdot\sqrt{5x^2+2x-3}=5x^2+4x-5\)
=>\(\left(x+1\right)\sqrt{5x^2+2x-3}=5x^2+2x-3+2x-2\)
=>\(\left(x+1\right)\sqrt{5x^2+2x-3}-\left(5x^2+2x-3\right)-\left(2x-2\right)=0\)
=>\(\sqrt{5x^2+2x-3}\left(x+1-\sqrt{5x^2+2x-3}\right)-2\left(x-1\right)=0\)
=>\(\sqrt{5x^2+2x-3}\cdot\dfrac{\left(x+1\right)^2-\left(5x^2+2x-3\right)}{x+1+\sqrt{5x^2+2x-3}}-2\left(x-1\right)=0\)
=>\(\sqrt{5x^2+2x-3}\cdot\dfrac{x^2+2x+1-5x^2-2x+3}{x+1+\sqrt{5x^2+2x-3}}-2\left(x-1\right)=0\)
=>\(\dfrac{\sqrt{5x^2+2x-3}}{x+1+\sqrt{5x^2-2x+3}}\cdot\left(-4x^2+4\right)-2\left(x-1\right)=0\)
=>\(\dfrac{2\sqrt{5x^2+2x-3}}{x+1+\sqrt{5x^2-2x+3}}\cdot\left(x^2-1\right)+\left(x-1\right)=0\)
=>\(\dfrac{2\sqrt{5x^2+2x-3}\cdot\left(x+1\right)\left(x-1\right)}{x+1+\sqrt{5x^2-2x+3}}+\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(\dfrac{2\sqrt{5x^2+2x-3}\cdot\left(x+1\right)}{x+1+\sqrt{5x^2-2x+3}}+1\right)=0\)
=>x-1=0
=>x=1(nhận)
AH
Akai Haruma
Giáo viên
30 tháng 11 2023
Lời giải:
a. Thể tích cái bánh: $6\times 8\times 3:2=72$ (cm3)
b.
Độ dài cạnh chéo miếng bánh: $\sqrt{6^2+8^2}=10$ (cm)
Diện tích vật liệu cần dùng chính là diện tích toàn phần của cái bánh và bằng:
$6.8+6.3+3.8+10.3=120$ (cm2)
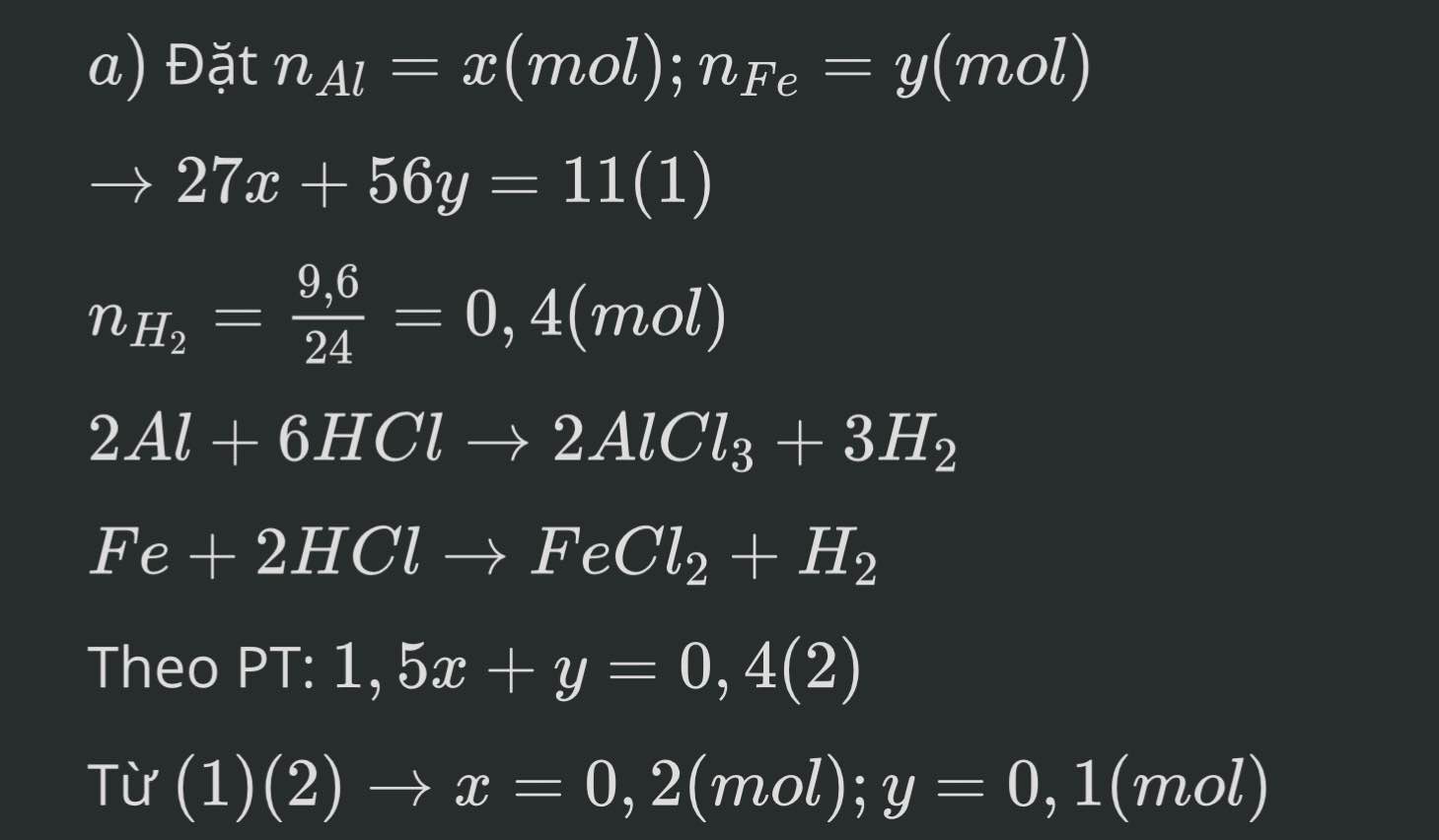
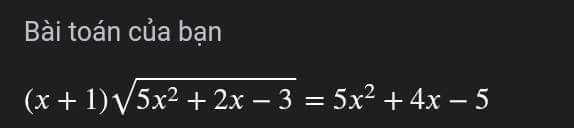
3)\(\sqrt{3m-2x}-2x-2=0\)
\(\Leftrightarrow3m-2x=4x^2+8x+4\) ( đk \(x\ge-1\) )
\(\Leftrightarrow4x^2+10x-3m+4=0\)
\(\Delta=10^2-4.4.\left(-3m+4\right)=100+48m-64=48m+36\)
để pt có nghiệm khi \(\Delta=0\Leftrightarrow48m+36=0\Leftrightarrow m=-\dfrac{3}{4}\)
vậy ..................