Tìm a , b \(\in\)N biết :
ƯCLN ( a,b ) = 10
BCNN ( a,b ) = 120
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
13 tháng 11 2023
a, b: Bạn xem lại đề.
c.
Vì $ƯCLN(a,b)=12$ và $a>b$ nên đặt $a=12x, b=12y$ với $x,y$ là stn, $x>y$, $(x,y)=1$. Khi đó:
$a+b=12x+12y=120\Rightarrow x+y=10$
Vì $x>y, (x,y)=1$ nên $x,y$ có thể nhận giá trị là:
$(x,y)=(9,1), (7,3)$
$\Rightarrow (a,b)=(108. 12), (84, 36)$
AH
Akai Haruma
Giáo viên
13 tháng 11 2023
d.
Vì $ƯCLN(a,b)=28$ và $a>b$ nên đặt $a=28x, b=28y$ với $x,y$ là stn, $x>y$, $(x,y)=1$. Khi đó:
$a+b=28x+28y=224$
$\Rightarrow x+y=8$
Vì $x>y$ và $(x,y)=1$ nên $x,y$ có thể nhận các giá trị là:
$(x,y)=(7,1), (5,3)$
$\Rightarrow (a,b)=(196, 28), (140, 84)$
PT
1
CM
24 tháng 11 2018
Vì (a,b) = 6 nên a = 6x, b = 6y, với (x,y)=1
Suy ra a.b=6x.6y = 36xy.
Lại có a.b = [a,b].(a,b) = 120.6 = 720
Suy ra 36xy = 720 => xy = 20
Giả sử x < y, và (x,y)=1 ta có các trường hợp sau:
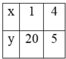
Từ đó suy ra a,b có các trường hợp sau:
PT
1
NM
0
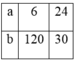
\(\hept{\begin{cases}\left(a,b\right)=10\\\left[a,b\right]=120\end{cases}}\Rightarrow\left(a,b\right)\left[a,b\right]=a\times b=10\times120=1200\left(a>b\right)\)
\(\left(a,b\right)=10\Rightarrow\hept{\begin{cases}a=10m\\b=10n\end{cases}\Rightarrow a\times b=10m\times10n=1200}\)
\(\Rightarrow100mn=1200\)\(\Rightarrow mn=1200\div100\)
\(\Rightarrow mn=12\left[\left(m,n\right)=1;m>n\right]\)
Sau đó tính m , n và tính a và b là xong