CMR:tồn tại 1 góc ngoài tam giác có số đo nhỏ hơn 120 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2021
\(\widehat{A}=180^0-120^0=60^0\\ \Rightarrow2\cdot60^0=120^0=3\widehat{B}\\ \Rightarrow\widehat{B}=40^0\\ \Rightarrow\widehat{BIA}=180^0-\widehat{IBA}-\widehat{IAB}=180^0-\dfrac{1}{2}\widehat{A}-\dfrac{1}{2}\widehat{B}=180^0-\dfrac{1}{2}\left(\widehat{A}+\widehat{B}\right)=180^0-\dfrac{1}{2}\cdot100^0=130^0\)
20 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
Gọi số đo góc ngoài của $\widehat {B}$ và $\widehat {C}$ lần lượt là `x, y`
Ta có:
$\widehat {x} + \widehat {B} = 180^0 (\text {Kề bù})$
`=> 120^0 +` $\widehat {B} = 180^0$
`=>` $\widehat {B} = 180^0 - 120^0 = 60^0$
Vậy, $\widehat {B} = 60^0$
Ta có:
$\widehat {y} + \widehat {C} = 180^0 (\text {Kề bù})$
`=>` $130^0 + \widehat {C} = 180^0$
`=>` $\widehat {C} = 180^0 - 130^0 = 50^0$
Vậy, $\widehat {C} = 50^0$
Xét `\Delta ABC:`
$\widehat {A} + \widehat {B} + \widehat {C} = 180^0 (\text {Đlí tổng 3 góc trong 1} \Delta)$
$\widehat {A} + 60^0 + 50^0 = 180^0$
`=>` $\widehat {A} = 70^0$
20 tháng 7 2023
Số đo `hat(B)` là: `180^o - 120^o = 60^o`.
Số đo `hat(C)` là: `180^o - 130^o = 50^o`.
Số đo `hat(A)` là: `180^o - 60^o - 50^o = 70^o`.
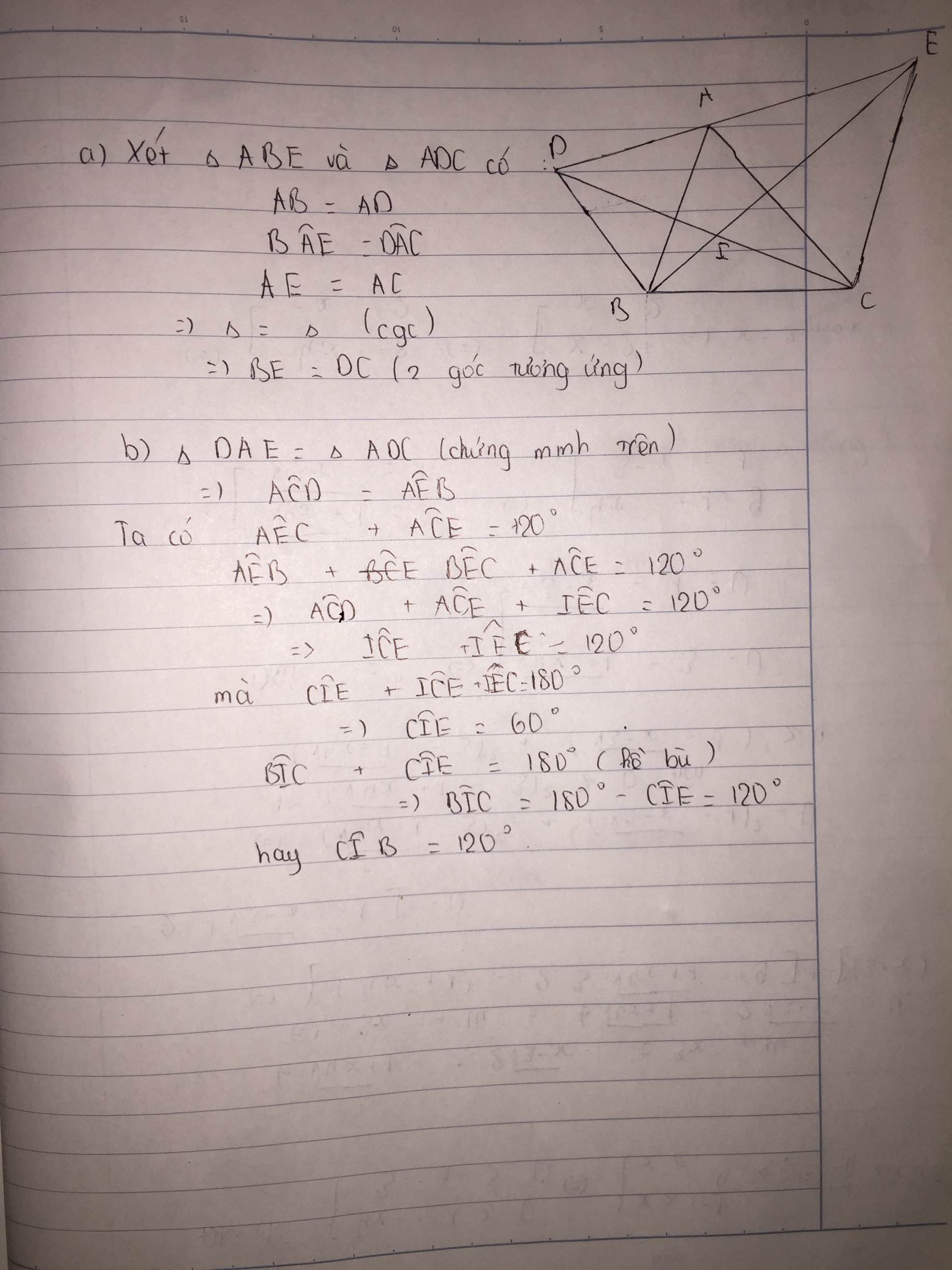
giả sử có 1 tam giác có góc ngoài > 120 độ => tổng các góc trong tam giác > 120 độ ( vô lí vì tổng 3 góc trong tam giác = 360 độ )
=> có 1 góc ngoài < 120 độ
Mình không biết có đúng không nha. Nếu đúng thì **** cho mình nha