Cho (P): y = \(x^2-3x+1\) và (d) : y = \(\left(2m^2+1\right)x+2\) và điểm M(3;3). Tìm m để (P) cắt (d) tại hai điểm phân biệt A,B sao cho tam giác MBA vuông cân tại M
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1 2022
Gọi \(A\left(x_1;x_1^2\right)\) và \(B\left(x_2;x_2^2\right)\) là 2 điểm thuộc (P) và đối xứng qua M
Do A; B đối xứng qua M
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2.\left(-1\right)\\x_1^2+x_2^2=2.5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=-2-x_1\\x_1^2+x_2^2=10\end{matrix}\right.\)
\(\Rightarrow x_1^2+\left(-2-x_1\right)^2=10\)
\(\Rightarrow2x_1^2+4x_1-6=0\Rightarrow\left[{}\begin{matrix}x_1=1\\x_1=-3\end{matrix}\right.\)
Vậy 2 điểm đó là \(\left(1;1\right)\) và \(\left(-3;9\right)\)
23 tháng 1 2022
Phương trình hoành độ giao điểm là:
\(x^2-\left(2m+1\right)x+m^2-1=0\)
\(\text{Δ}=\left(2m+1\right)^2-4\left(m^2-1\right)\)
\(=4m^2+4m+1-4m^2+4=4m+5\)
Để (P) cắt (d) tại hai điểm nằm về hai phía của trục tung thì \(m^2-1< 0\)
hay -1<m<1
21 tháng 6 2023
PTHĐGĐ là:
x^2-(m-1)x-m^2+2m-3=0
a*c=-m^2+2m-3=-(m^2-2m+3)
=-(m^2-2m+1+2)
=-(m-1)^2-2<0
=>(P) luôn cắt (d) tại hai điểm phân biệt
1 tháng 1 2022
b: Phương trình hoành độ giao điểm là:
\(x^2-2\left(m-1\right)x-m^2-2m=0\)
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(-m^2-2m\right)\)
\(=4m^2-8m+4+4m^2+8m=8m^2+4>0\)
Vậy: Phương trình luôn có hai nghiệm phân biệt
\(x_1^2+x_2^2+4x_1x_2=36\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+2x_1x_2=36\)
\(\Leftrightarrow\left[2\left(m-1\right)\right]^2+2\left(-m^2-2m\right)=36\)
\(\Leftrightarrow4m^2-8m+4-2m^2-4m-36=0\)
\(\Leftrightarrow2m^2-12m-32=0\)
\(\Leftrightarrow\left(m-8\right)\left(m+2\right)=0\)
hay \(m\in\left\{8;-2\right\}\)
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Lời giải:
a. Với $m=1$ thì ptđt $(d)$ là: $y=x+1$
b. Trung điểm của 2 đường thẳng??? Đường thẳng thì làm gì có trung điểm hả bạn? Đoạn thẳng thì có.
c. $(d)$ cắt $y=x-2$ tại điểm có hoành độ $-1$
$\Leftrightarrow$ PT hoành độ giao điểm $(2-m)x+2m-1-(x-2)=0$ nhận $x=-1$ là nghiệm
$\Leftrightarrow (2-m)(-1)+2m-1-(-1-2)=0$
$\Leftrightarrow m=0$
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
1.
Phương trình hoành độ giao điểm:
\(2x-3=x+1\Rightarrow x=4\)
\(\Rightarrow y=5\)
Vậy tọa độ giao điểm là \(\left(4;5\right)\)
2.
Hai đường thẳng cắt nhau tại A khi chúng không song song nhau và cùng đi qua A
\(\Rightarrow\left\{{}\begin{matrix}2m-1\ne2n\\\left(2m-1\right).1+n+2=-2\\2n.1+2m-3=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-1\ne2n\\2m+n=-3\\2m+2n=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}n=4\\m=-\dfrac{7}{2}\end{matrix}\right.\)
13 tháng 12 2023
a: Để (d1) và (d2) cắt nhau thì \(2m+1\ne m+2\)
=>\(2m-m\ne2-1\)
=>\(m\ne1\)
b: Khi m=-1 thì (d1): \(y=\left(2-1\right)x+1=x+1\)
Khi m=-1 thì (d2): \(y=\left(1-2\right)x+2=-x+2\)
Vẽ đồ thị:
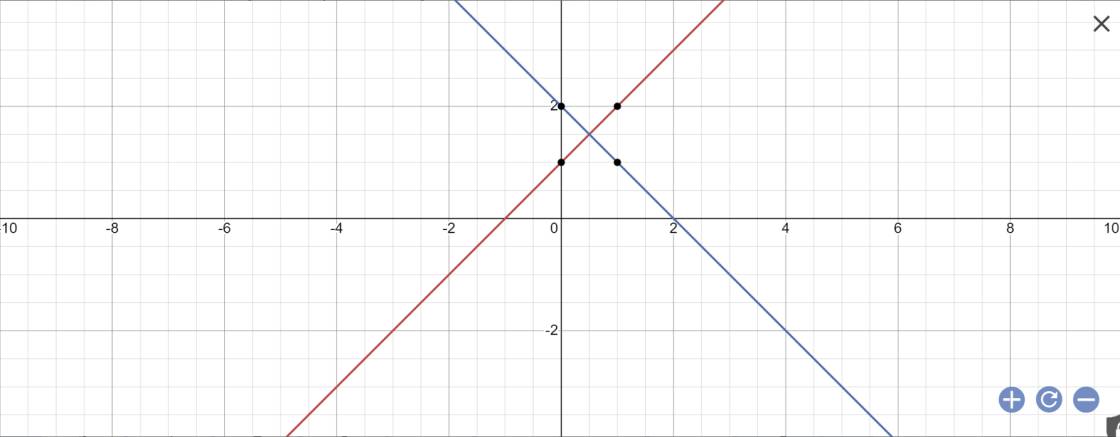
Phương trình hoành độ giao điểm là:
x+1=-x+2
=>x+x=2-1
=>2x=1
=>\(x=\dfrac{1}{2}\)
Thay x=1/2 vào y=x+1, ta được:
\(y=\dfrac{1}{2}+1=\dfrac{3}{2}\)
c:
(d1): y=(m+2)x+1
=>(m+2)x-y+1=0
Khoảng cách từ A(1;3) đến (d1) là:
\(d\left(A;\left(d1\right)\right)=\dfrac{\left|1\left(m+2\right)+3\cdot\left(-1\right)+1\right|}{\sqrt{\left(m+2\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|m\right|}{\sqrt{\left(m+2\right)^2+1}}\)
Để d(A;(d1)) lớn nhất thì m+2=0
=>m=-2
Vậy: \(d\left(A;\left(d1\right)\right)_{max}=\dfrac{\left|-2\right|}{\sqrt{\left(-2+2\right)^2+1}}=\dfrac{2}{1}=2\)
3 tháng 11 2016
a/ Để hàm số này là hàm bậc nhất thì
\(\hept{\begin{cases}\left(3n-1\right)\left(2m+3\right)=0\\4m+3\ne0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}n=\frac{1}{3}\\m=\frac{-3}{2}\end{cases}}\)
Các câu còn lại làm tương tự nhé bạn
AH
Akai Haruma
Giáo viên
27 tháng 4 2023
Lời giải:
PT hoành độ giao điểm:
$x^2-(2x+2m-1)=0$
$\Leftrightarrow x^2-2x+(1-2m)=0(*)$
Để $(P)$ và $(d)$ cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì pt $(*)$ có 2 nghiệm pb $x_1,x_2$
Điều này xảy ra khi $\Delta'=1-(1-2m)=2m>0\Leftrightarrow m>0$
Theo định lý Viet:
$x_1+x_2=2$
$x_1x_2=1-2m$
Khi đó:
$x_2^2(x_1^2-1)+x_1^2(x_2^2-1)=8$
$\Leftrightarrow 2(x_1x_2)^2-(x_1^2+x_2^2)=8$
$\Leftrightarrow 2(x_1x_2)^2-[(x_1+x_2)^2-2x_1x_2]=8$
$\Leftrightarrow 2(1-2m)^2-[2^2-2(1-2m)]=8$
$\Leftrightarrow 8m^2-12m=8$
$\Leftrightarrow 2m^2-3m-2=0$
$\Leftrightarrow (m-2)(2m+1)=0$
$\Leftrightarrow m=2$ hoặc $m=\frac{-1}{2}$
Vì $m>0$ nên $m=2$
Lời giải:
Đặt \(2m^2+1=t\)
Gọi \(A(x_A, tx_A+2); B(x_B; tx_B+2)\)
PT hoành độ giao điểm $(P)$ và $(d)$ là:
\(x^2-3x+1-(tx+2)=0\)
\(\Leftrightarrow x^2-(t+3)x-1=0\)
Theo định lý Viete: \(\left\{\begin{matrix} x_A+x_B=t+3\\ x_Ax_B=-1\end{matrix}\right.\)
Để thỏa mãn tam giác $MBA$ vuông cân tại $M$ thì:
\(\left\{\begin{matrix} |\overrightarrow{MA}|=|\overrightarrow{MB}|\\ \overrightarrow{MA}.\overrightarrow{MB}=\overrightarrow {0}\end{matrix}\right.\)
Trước hết : \(\overrightarrow{MA}.\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow (x_A-3, tx_A-1)(x_B-3, tx_B-1)=\overrightarrow{0}\)
\(\Leftrightarrow (x_A-3)(x_B-3)+(tx_A-1)(tx_B-1)=0\)
\(\Leftrightarrow x_Ax_B-3(x_A+x_B)+9+t^2x_Ax_B-t(x_A+x_B)+1=0\)
\(\Leftrightarrow -1-3(t+3)+9-t^2-t(t+3)+1=0\)
\(\Leftrightarrow -2t^2-6t=0\Leftrightarrow t=0\) hoặc $t=-3$
Hiển nhiên \(t=2m^2+1>0\) với mọi $m$ nên vô lý
Do đó không tồn tại $m$ thỏa mãn.