Question

[Ichigo Hollow]

tìm m để phương trình 2x²+(3m-2)x-(5-2m)=0 có 2 nghiệm phân biệt x1,x2 sao cho 3x₁+2x₂=0

Answer 1

[Rimuru tempest]

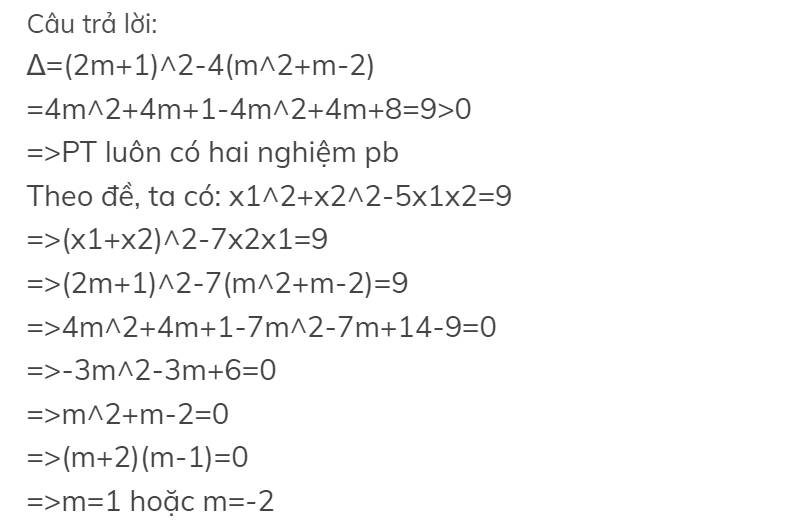
\(\Delta=b^2-4ac\)

\(\Delta=\left(3m-2\right)^2-4.2.\left(2m-5\right)=9m^2-12m+4-16m+40\)

\(\Delta=9m^2-28m+44\)

Để pt có 2 nghiệm phân biệt \(\Leftrightarrow\Delta\ge0\Leftrightarrow9m^2-28m+44\ge0\left(lđ\right)\)

theo vi-ét ta có:

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{b}{a}=\dfrac{3m-2}{2}\left(1\right)\\x_1.x_2=-\dfrac{c}{a}=\dfrac{5-2m}{2}\left(2\right)\end{matrix}\right.\)

ta có \(3x_1+2x_2=0\left(3\right)\)

từ (1)(3) ta có hệ

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3m-2}{2}\\3x_1+2x_2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=3m-2\\3x_1+2x_2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1=2-3m\\x_2=-\dfrac{3}{2}x_1\end{matrix}\right.\)(lấy dưới trừ trên)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1=2-3m\\x_2=-\dfrac{3}{2}\left(2-3m\right)\end{matrix}\right.\)

ta có \(x_1.x_2=\dfrac{5-2m}{2}\)

\(\Leftrightarrow-\dfrac{3}{2}\left(2-3m\right)\left(2-3m\right)=\dfrac{5-2m}{2}\)

\(\Leftrightarrow-3\left(9m^2-12m+4\right)=5-2m\)

\(\Leftrightarrow-27m^2+36m-12=5-2m\)

\(\Leftrightarrow-27m^2+38m-17=0\) ( vô lý)

vậy pt vô nghiệm