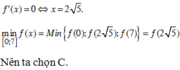một đèn tìm kiếm xoay trong một ngọn hải đăng cách bờ 2 km đang chiếu theo một người di dọc bờ biển, khi người đi bộ còn cách 1 km so với điểm trên bờ mà gần nhất với ngọn hải đăng, thì đèn tìm kiếm đang xoay với tốc độ pi/2 rad/giờ. hỏi người đi bộ đang đi với vận tốc bao nhiêu tại thời điểm này?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Sau t giây điểm M quét được một góc lượng giác có số đo là: \(\alpha = \frac{\pi }{{10}}t\) rad.
Xét tam giác HOM vuông tại O có:
\(MO = tan\alpha .1 = \tan \left( {\frac{\pi }{{10}}t} \right)\).
Vậy tọa độ \({y_M} = \tan \left( {\frac{\pi }{{10}}t} \right)\).
b) Xét \(\tan \left( {\frac{\pi }{{10}}t} \right) = - 1\)
\(\begin{array}{l} \Leftrightarrow \tan \left( {\frac{\pi }{{10}}t} \right) = \tan \left( { - \frac{\pi }{4}} \right)\\ \Leftrightarrow \frac{\pi }{{10}}t = - \frac{\pi }{4} + k\pi \\ \Leftrightarrow t = - \frac{5}{2} + 10k,k \in \mathbb{Z}.\end{array}\)
Vì \(t \ge 0\) nên tại các thời điểm \(t = - \frac{5}{2} + 10k,k \in \mathbb{Z},k \ge 1\) thì đèn hải đăng chiếu vào ngôi nhà.

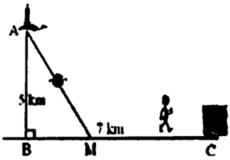
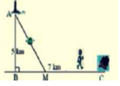
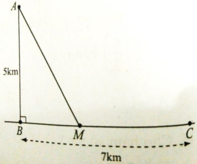
Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có: \(AM = \sqrt {A{B^2} + B{M^2}} \)\( = \sqrt {16 + {x^2}} \left( {km} \right)\)
Thời gian từ A đến M là: \(\frac{{\sqrt {16 + {x^2}} }}{3}\left( h \right)\)
Thời gian từ M đến C là: \(\frac{{7 - x}}{5}\left( h \right)\)
Tổng thời gian từ A đến C là 148 phút nên ta có:
\(\begin{array}{l}\frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{148}}{{60}}\\ \Leftrightarrow \frac{{\sqrt {16 + {x^2}} }}{3} + \frac{{7 - x}}{5} = \frac{{37}}{{15}}\\ \Leftrightarrow \frac{{5\sqrt {16 + {x^2}} }}{{15}} + \frac{{3.\left( {7 - x} \right)}}{{15}} = \frac{{37}}{{15}}\\ \Leftrightarrow 5\sqrt {16 + {x^2}} + 3.\left( {7 - x} \right) = 37\\ \Leftrightarrow 5\sqrt {16 + {x^2}} = 16 + 3x\\ \Leftrightarrow 25.\left( {16 + {x^2}} \right) = 9{x^2} + 96x + 256\\ \Leftrightarrow 16{x^2} - 96x + 144 = 0\\ \Leftrightarrow x = 3\left( {tm} \right)\end{array}\)
Vậy khoảng cách từ vị trí B đến M là 3 km.

Đáp án A
Phương pháp: Sử dụng phương pháp hàm số.
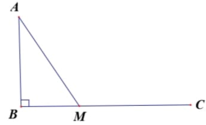
Cách giải: Gọi độ dài đoạn MB là x ![]()
Tam giác ABM vuông tại B => ![]()
Thời gian người đó đi từ A tới C: 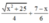
Xét hàm số f(x) 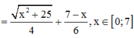

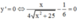
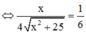
![]()
![]()
=> x = 2 5
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là 2 5

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
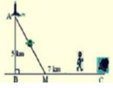
Đặt BM= x , CM =7-x-> A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
Đặt BM= x , CM =7-x ⇒ A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5


Áp dụng kết quả bài 34 ta có:
+ MT2 = MA.MB
MA = 40m = 0,04km ;
MB = MA + AB = MA + 2R = 12800,04 km.
⇒ MT ≈ 22,63 km
+ M’T2 = M’A’.M’B’
M’A’ = 10m = 0,01km ;
M’B’ = M’A’ + A’B’ = M’A’ + 2R = 12800,01 km
⇒ M’T ≈ 11,31 km
⇒ MM’ = MT + M’T = 33,94 ≈ 34 km .
Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

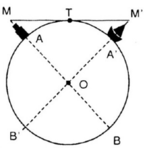
Áp dụng kết quả bài 34 ta có:
+ M T 2 = M A . M B
MA = 40m = 0,04km ;
MB = MA + AB = MA + 2R = 12800,04 km.
⇒ MT ≈ 22,63 km
+ M ’ T 2 = M ’ A ’ . M ’ B ’
M’A’ = 10m = 0,01km ;
M’B’ = M’A’ + A’B’ = M’A’ + 2R = 12800,01 km
⇒ M’T ≈ 11,31 km
⇒ MM’ = MT + M’T = 33,94 ≈ 34 km .
Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

Đặt BM = x (0 ≤ x ≤ 7) => MC = 7 - x. Áp dụng định lí Py-ta-go cho tam giác vuông ABM có
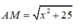
Thời gian đi từ A đến M là
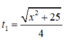
thời gian đi từ M đến C là
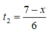
Tổng thời gian đi từ A đến C là
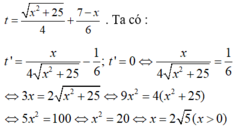
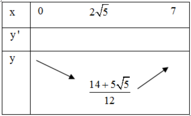
Bảng biến thiên
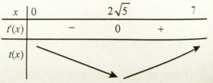
Để người đó đến kho nhanh nhất thì thời gian đi cần ít nhất, tức t đạt giá trị nhỏ nhất. Dựa vào bảng biến thiên ta thấy t đạt giá trị nhỏ nhất tại x = 2√5 ≈ 4,5
Vậy vị trí điểm M cách B một khoảng là 4,5km thì người đó đến kho là nhanh nhất.
Chọn B