Cho tam giác ABC vuông tại A. Đườn g cao AH. Biết HB = 18, HC = 32. Tính AC và AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 7 2023
1: AB/AC=5/7
=>HB/HC=(AB/AC)^2=25/49
=>HB/25=HC/49=k
=>HB=25k; HC=49k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>1225k^2=15^2=225
=>k^2=9/49
=>k=3/7
=>HB=75/7cm; HC=21(cm)
UT
4 tháng 4 2021
tự vẽ hình
ta có <HBA+<BAH= 90\(^0\)(vì tam giác ABH vg tại H)
Có <BAH+ <HAC= 90\(^0\)(vì tam giác ABC vg tại A)
=> <HBA=<HAC
Xét tam giác BAH và ACH
<BHA=<AHC\(\left(90^0\right)\)
<ABH=<HAC
=> Tam giác BAH đồng dạng với tam giác ACH
=> BH/AH=AH/CH=> AH^2= BH*CH=4*9=36 cm
b, ta có BC=BH+CH=4+9=13 cm
S(ABC) = AH*BC=36*13=468 cm\(^2\)
12 tháng 9 2021
Bài 2:
Ta có: \(\dfrac{HB}{HC}=\dfrac{1}{3}\)
nên HC=3HB
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB^2=48\)
\(\Leftrightarrow HB=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\cdot HB=16\sqrt{3}\left(cm\right)\)
12 tháng 9 2021
Bài 1:
ta có: \(AB=\dfrac{1}{2}AC\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{1}{4}\)
\(\Leftrightarrow HC=4HB\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=1\left(cm\right)\)
\(\Leftrightarrow HC=4\left(cm\right)\)
hay BC=5(cm)
Xét ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=HC\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)
26 tháng 9 2021
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
LT
22 tháng 10 2021
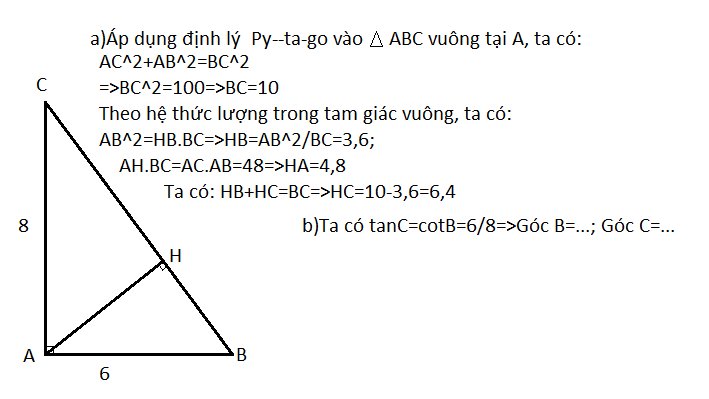
áp dụng định lí pytago vào tg vuông ABC
=>AB2+AC2=BC2
=>BC=√7,22+9,62
=>BC=12cm
áp dụng định lí 1
=>AC2=HC.BC
=>HC=AC2/BC=9,62/12=7,68cm
lại có HB+HC=BC
=>HC=BC-HC=12-7,68=4,32cm
22 tháng 10 2021
Cảm ơn nha mấy hôm nay hỏi ko có ai trả lời may là có bạn
19 tháng 8 2021
b: Ta có: \(\widehat{ADC}+\widehat{HAD}=90^0\)
\(\widehat{CAD}+\widehat{DAB}=90^0\)
mà \(\widehat{HAD}=\widehat{DAB}\)
nên \(\widehat{ADC}=\widehat{CAD}\)
Xét ΔADC có \(\widehat{ADC}=\widehat{CAD}\)
nên ΔADC cân tại C
2 tháng 12 2021
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
25 tháng 5 2023
AB/AC=4/3
=>HB/HC=16/9
=>HB/16=HC/9=k
=>HB=16k; HC=9k
AH^2=HB*HC
=>144k^2=24^2=576
=>k=2
=>HB=32cm; HC=18cm
AB=căn 32*50=40cm
AC=căn 18*50=30cm