Cho hàm số y =\(\dfrac{1}{2}\)x - 1 (d)
a)Vẽ đồ thị hàm số trên
b)Tính khoảng cách từ O đến đường thẳng d
-giúp mình với ạ-
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:Thay x=-2 và y=0 vào (d), ta được:
-2(m-1)+4=0
=>-2(m-1)=-4
=>m-1=2
=>m=3
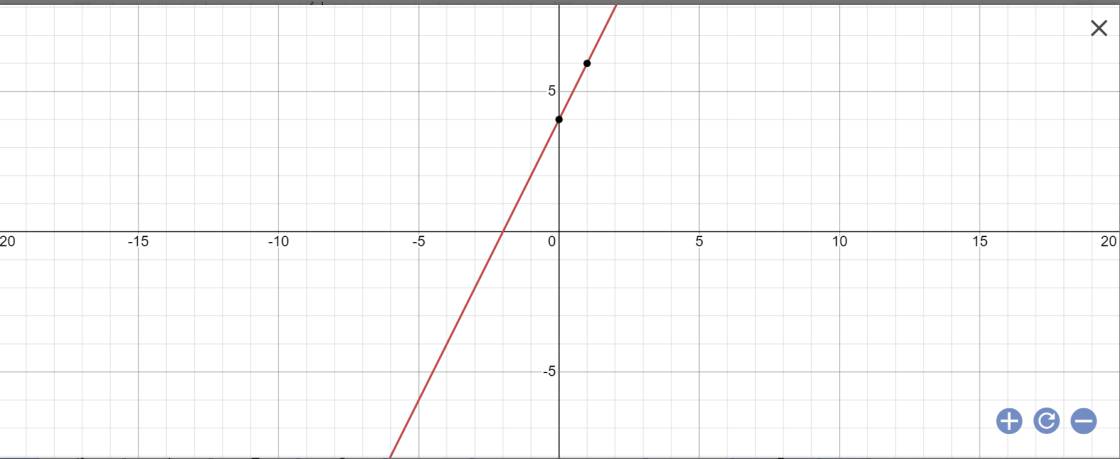
b: (d): y=2x+4

Để hàm số y=(1-m)x+1 là hàm số bậc nhất thì \(1-m\ne0\)
\(\Leftrightarrow m\ne1\)
a) Để hàm số y=(1-m)x+1 đồng biến trên R thì 1-m>0
\(\Leftrightarrow-m>-1\)
hay m<1
Kết hợp ĐKXĐ, ta được: m<1
Vậy: Để hàm số y=(1-m)x+1 đồng biến trên R thì m<1
c)
Thay m=2 vào hàm số y=(1-m)x+1, ta được:
y=(1-2)x+1
\(\Leftrightarrow y=-x+1\)Gọi A(xA,yA) và B(xB,yB) lần lượt là giao điểm của đồ thị hàm số y=-x+1 với trục Ox và trục Oy
Vì A(xA,yA) là giao điểm của đồ thị hàm số y=-x+1 với trục Ox nên yA=0
Thay y=0 vào hàm số y=-x+1, ta được:
-x+1=0
\(\Leftrightarrow-x=-1\)
hay x=1
Vậy: A(1;0)
Vì B(xB,yB) là giao điểm của đồ thị hàm số y=-x+1 với trục Oy nên xB=0
Thay x=0 vào hàm số y=-x+1, ta được:
y=-0+1=1
Vậy: B(0;1)
Độ dài đoạn thẳng OB là:
\(OB=\sqrt{\left(x_O-x_B\right)^2+\left(y_O-y_B\right)^2}\)
\(\Leftrightarrow OB=\sqrt{\left(0-0\right)^2+\left(0-1\right)^2}=1\)(đvđd)
Độ dài đoạn thẳng OA là:
\(OB=\sqrt{\left(x_O-x_A\right)^2+\left(y_O-y_A\right)^2}\)
\(\Leftrightarrow OB=\sqrt{\left(0-1\right)^2+\left(0-0\right)^2}=1\)(đvđd)
Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}\)
\(\Leftrightarrow AB=\sqrt{\left(1-0\right)^2+\left(0-1\right)^2}=\sqrt{2}\)(đvđd)
Ta có: \(AB^2=\left(\sqrt{2}\right)^2=2\)
\(OA^2+OB^2=1^2+1^2=2\)
Do đó: \(AB^2=OA^2+OB^2\)(=2)
Xét ΔOAB có \(AB^2=OA^2+OB^2\)(cmt)
nên ΔOAB vuông tại O(Định lí Pytago đảo)
Kẻ OH⊥AB tại H
⇒OH là khoảng cách từ O đến (d)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOAB vuông tại O có OH là đường cao ứng với cạnh huyền AB, ta được:
\(OH\cdot AB=OA\cdot OB\)
\(\Leftrightarrow OH\cdot\sqrt{2}=1\cdot1=1\)
hay \(OH=\dfrac{\sqrt{2}}{2}\)(đvđd)
Vậy: Khoảng cách từ O đến (d) là \(OH=\dfrac{\sqrt{2}}{2}\)

a: 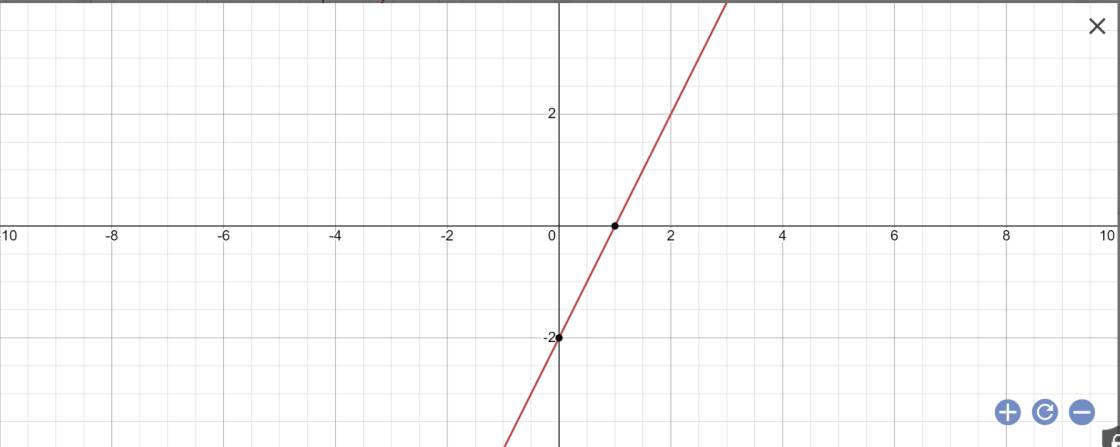
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}m+1=2\\6< >-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=2
=>m=1
c:
(d'): y=(m+1)x+6
=>(m+1)x-y+6=0
Khoảng cách từ O đến (d') là:
\(d\left(O;\left(d'\right)\right)=\dfrac{\left|0\cdot\left(m+1\right)+0\cdot\left(-1\right)+6\right|}{\sqrt{\left(m+1\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}\)
Để \(d\left(O;\left(d'\right)\right)=3\sqrt{2}\) thì \(\dfrac{6}{\sqrt{\left(m+1\right)^2+1}}=3\sqrt{2}\)
=>\(\sqrt{\left(m+1\right)^2+1}=\sqrt{2}\)
=>\(\left(m+1\right)^2+1=2\)
=>\(\left(m+1\right)^2=1\)
=>\(\left[{}\begin{matrix}m+1=1\\m+1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)

a/ Hai hàm số có đồ thị // với nhau khi
\(\hept{\begin{cases}m-2=1\\3\ne0\end{cases}}\Leftrightarrow m=3\)
b/ Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ
\(\hept{\begin{cases}y=x+3\\y=2x+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=5\end{cases}}\)
c/ Gọi điểm mà đường thẳng luôn đi qua là M(a,b) ta thế vào hàm số được
\(b=ma+3\)
\(\Leftrightarrow ma+3-b=0\)
Để phương trình này không phụ thuôc m thì
\(\hept{\begin{cases}a=0\\3-b=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=0\\b=3\end{cases}}\)
Tọa độ điểm cần tìm là M(0, 3)
d/ Ta có khoản cách từ O(0,0) tới (d) là 1
\(\Rightarrow=\frac{\left|0-0m-3\right|}{\sqrt{1^2+m^2}}=\frac{3}{\sqrt{1+m^2}}=1\)
\(\Leftrightarrow\sqrt{1+m^2}=3\)
\(\Leftrightarrow m^2=8\)
\(\Leftrightarrow\orbr{\begin{cases}m=2\sqrt{2}\\m=-2\sqrt{2}\end{cases}}\)

\(b,\) PT giao Ox và Oy:
\(y=0\Leftrightarrow x=2\Leftrightarrow A\left(2;0\right)\Leftrightarrow OA=2\\ x=0\Leftrightarrow y=-4\Leftrightarrow B\left(0;-4\right)\Leftrightarrow OB=4\)
Gọi H là chân đường cao từ O đến (d)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{16}=\dfrac{5}{16}\)
\(\Leftrightarrow OH^2=\dfrac{16}{5}\Leftrightarrow OH=\dfrac{4}{\sqrt{5}}\left(cm\right)\)
Vậy k/c là \(\dfrac{4}{\sqrt{5}}\left(cm\right)\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne-4\\0a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)

c: y=(m-1)x+4
=>\(\left(m-1\right)x-y+4=0\)
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-1\right)+0\cdot\left(-1\right)+4\right|}{\sqrt{\left(m-1\right)^2+\left(-1\right)^2}}=\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}\)
Để \(d\left(O;\left(d\right)\right)=2\) thì \(\dfrac{4}{\sqrt{\left(m-1\right)^2+1}}=2\)
=>\(\sqrt{\left(m-1\right)^2+1}=2\)
=>\(\left(m-1\right)^2+1=4\)
=>\(\left(m-1\right)^2=3\)
=>\(m-1=\pm\sqrt{3}\)
=>\(m=\pm\sqrt{3}+1\)
x=0 => y=-1
y=0 => x=2
b)Ox=2
Oy=1 Áp dụng hệ thức lượng \(\dfrac{1}{oh^2}=\dfrac{1}{\text{ox}^2}+\dfrac{1}{oy^2}=\dfrac{1}{4}+\dfrac{1}{1}=\dfrac{5}{4}\)\(\Rightarrow oh^2=\dfrac{4}{5}\Rightarrow oh=\dfrac{2\sqrt{5}}{5}\)