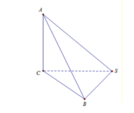
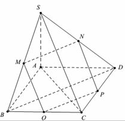
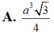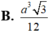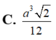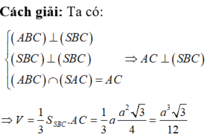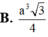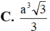1. Cho hình chóp S.ABCD có SB=SC=BC=CA=a. Hai mặt (ABC) và (ASC) cùng vuông góc với (SBC). Tính thể tích hình chóp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 5 2018
Đáp án B
Phương pháp: Công thức tính thể tích khối chóp V = 1 3 S . h với S là diện tích đáy,h là chiều cao.
Chú ý tính chất hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng đó.
Cách giải: Ta có: A B C ⊥ S B C S B C ⊥ S B C A B C ∩ S A C = A C ⇒ A C ⊥ S B C
⇒ V = 1 3 S S B C . A C = 1 3 a a 2 3 4 = a 3 3 12
CM
14 tháng 6 2019
Đáp án D
Do hai mặt phẳng (ABC) và (ASC) cùng vuông góc với (SBC)
nên A C ⊥ S B C .
Lại có: S A B C = a 2 3 4 ; A C = a ⇒ V A . S B C = 1 3 A C . S S B C = a 3 3 12 .
CM
13 tháng 5 2018
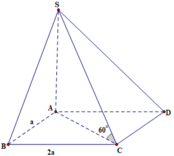
+Vì S A B ⊥ A B C D , S A D ⊥ A B C D mà S A B ∩ S A D = S A nên S A là đường cao của khối chóp
+ Xét tam giác vuông S A C
S A = tan 60 o . A C = 3 . a . 5 = a 15
CM
6 tháng 3 2019
Chọn A.
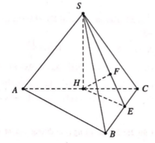
Dựng SH ⊥ AC , do ( SAC ) ⊥ ( ABC ) nên SH ⊥ ( ABC ) ; AC = 2 a . Dựng HE ⊥ BC ; HF ⊥ SE ⇒ d ( H ; ( SBC ) ) = HF . ΔSAC = ΔBCA ⇒ ΔSAC vuông tại S .
Dễ thấy tan ACB ^ = 1 3 ⇒ ACB ^ = 30 o = SAC ^ HC = SCcos 60 o = a 2 ; HE = HCsin 30 o = a 4 ; SH = a 3 2 . Do AC = 4 HC ⇒ d A = 4 d H = 4 . SH . HE SH 2 + HE 2 = 2 39 13 Do đó Sinα = d A SA = 2 13 .