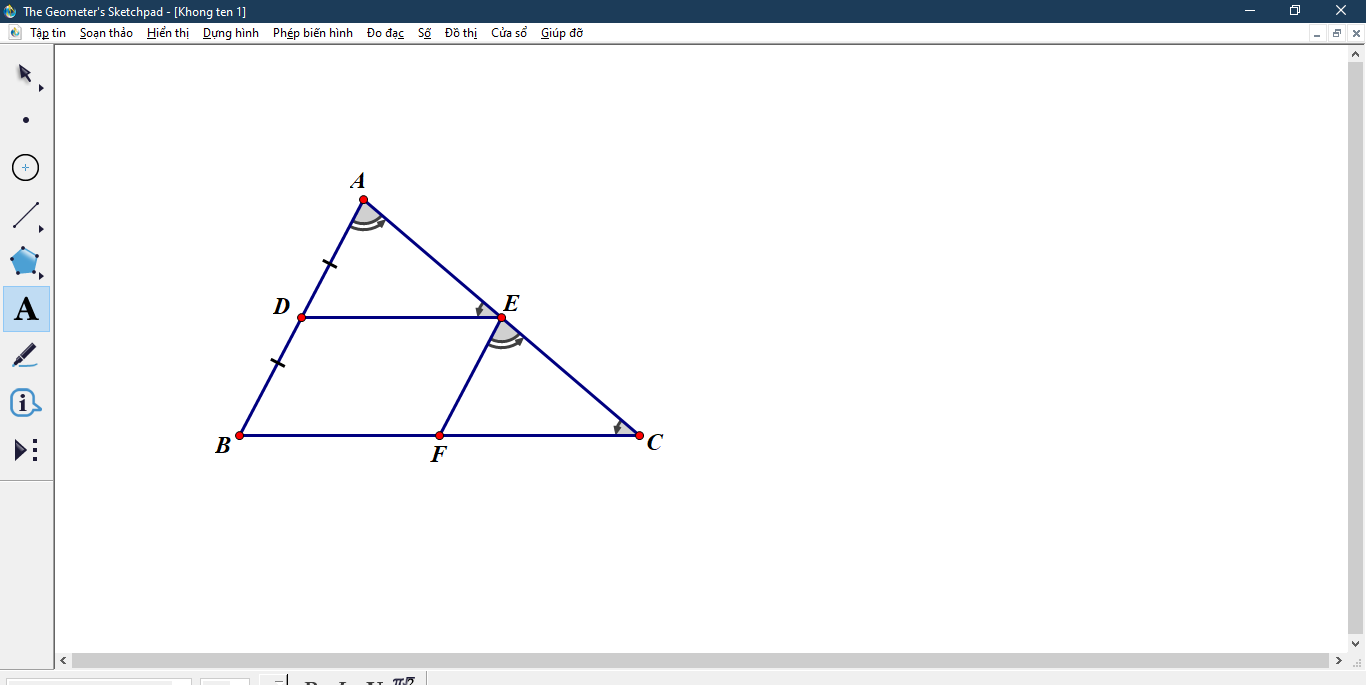
Cho tam giác ABC láy D là TĐ của BC. Qua D kẻ đường thẳng vuông góc với BC cắt A ở E. Đường thẳng qua E song song AB cắt BC ở F
a) Chứng minh: AD = EF
b) tam giác ADE = tam giác EFC = tam giác DBF
c) BC = 2DE, AB =2EF, AC=2DF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC

a)Nối D với F. Xét \(\Delta BDF\) và \(\Delta FDE\) ta có:
\(\widehat{BDF}=\widehat{DFE}\) (so le trong (Vì AB//EF (gt)))
DF cạnh chung
\(\widehat{DFB}=\widehat{FDE}\) (so le trong (Vì DE//BC (gt)))
\(\Rightarrow\Delta BDF\)\(=\Delta FDE\) (g.c.g)
\(\Rightarrow DB=EF\) (2 cạnh tương ứng )
Mà \(DB=DA\) (D là trung điểm AB)
Suy ra AD=EF
b)Xét \(\Delta ADE\) và \(\Delta EFC\:\) ta có:
\(\widehat{ADE}=\widehat{CFE}\) (\(=\widehat{BAC}\); đồng vị của DE//BC và EF//AB)
\(AD=EF\) (cmt)
\(\widehat{DAE}=\widehat{FEC}\) (đồng vị của DE//BC)
\(\Rightarrow\Delta ADE=\Delta EFC\) (g.c.g)
c)Vì \(\Delta ADE=\Delta EFC\) (cmt)
Suy ra \(AE=EC\) (2 cạnh tương ứng )

Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng :
a) AD = EF
b) Tam giác ADE = Tam giác EFC= tam giác DBF
c) BC= 2 lần DE

D với F. Xét ΔBDF và ΔFDE ta có:
ˆBDF=^DFE (so le trong (Vì AB//EF (gt))
DF cạnh chung
ˆDFB=ˆFDE(so le trong (Vì DE//BC (gt))
⇒ΔBDF=ΔFDE (g.c.g)
⇒DB=EF (2 cạnh tương ứng )
Mà DB=DA (D là trung điểm AB)
Suy ra AD=EF
b)Xét ΔADE và ΔEFC ta có:
ˆADE=ˆCFE (=ˆBAC; đồng vị của DE//BC và EF//AB)
AD=EF (cmt)
ˆDAE=ˆFEC(đồng vị của DE//BC)
⇒ΔADE=ΔEFC (g.c.g)
c)Vì ΔADE=ΔEFC (cmt)
Suy ra AE=EC (2 cạnh tương ứng )
HT

Xét \(\Delta ABC\) có AD=DB;DE//BC nên AE=EC hay E là trung điểm AC
Xét \(\Delta ADE\) và \(\Delta EFC\) có:
\(\left\{{}\begin{matrix}\widehat{DAE}=\widehat{FEC}\\AE=EC\left(cmt\right)\\\widehat{AED}=\widehat{ECF}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ADE\) \(=\) \(\Delta EFC\)\(\left(g.c.g\right)\)
Tick hộ nha
Vì AD=BD và d//BC
=> E là trung điểm của AC
=> AE = EC
Vì DE//BC
=> \(\widehat{AED}=\widehat{ECF}\) (2 góc đồng vị)
Vì ÈF//AB
\(\Rightarrow\widehat{DAE}=\widehat{FEC}\) (2 góc đồng vị)
Xét ΔADE và ΔECF có;
\(\widehat{AED}=\widehat{ECF}\) (cmt)
AE = EC
\(\widehat{DAE}=\widehat{FEC}\) (cmt)
=> ΔADE = ΔECF (g-c-g)

a. Nối DD và FF
Xét ΔBDFΔBDF và ΔDEFΔDEF , ta có :
DF=DFDF=DF ( cạnh chung )
ˆBDF=ˆDEFBDF^=DEF^ ( vì AB//EFAB//EF )
ˆDFB=ˆFDEDFB^=FDE^ ( vì DE//BCDE//BC )
⇒ΔBDF=ΔFDE(g.c.g)⇒ΔBDF=ΔFDE(g.c.g)
⇒DB=EF⇒DB=EF ( hai cạnh tương ứng )
Mà AD=DB⇒AD=EFAD=DB⇒AD=EF
b. Xét ΔADEΔADE và ΔEFCΔEFC , ta có :
ˆA=ˆFECA^=FEC^ ( vì AB//EFAB//EF )
AD=EFAD=EF ( theo câu a )
ˆADE=ˆEFC(=ˆB)ADE^=EFC^(=B^)
⇒ΔADE=ΔEFC(g.c.g)