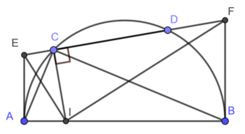
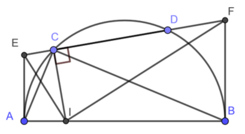
Bài 1 : a) Cho nửa đường tròn tâm O , đường kính AB . Vẽ dây CD bất kì khác AB . Từ C và D lần lượt kẻ các đường vuông góc CD , các đường này cắt AB thứ tự tại E và F . Chứng minh AF=BE
b) Cho nửa đường tròn (O) , đường kính MN. Trên MN lấy 2 điểm A và B sao cho AM=BN. Qua A và B kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn (O) lần lượt tại E và F . Chứng minh AE và BF vuông góc với EF
Gợi ý : a) Kẻ OM⊥CD tại M
b) Kẻ OM song song AE song song BF(M∈ EF)