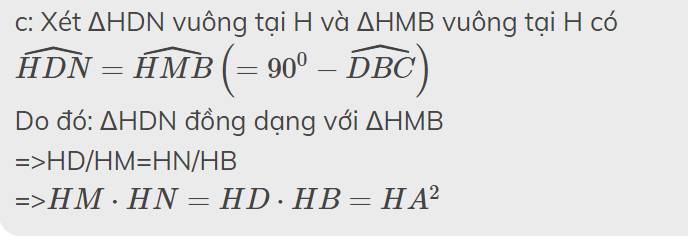cho hình chữ nhật ABCD , kẻ AH vuông góc với BD , biết HD=9cm , HB=16 cm. Tính AB, BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 9 2021
b: Xét ΔADM vuông tại D có DH là đường cao ứng với cạnh huyền AM
nên \(AH\cdot AM=AD^2\left(1\right)\)
Xét ΔADB vuông tại A có AH là đường cao ứng với cạnh huyền DB
nên \(DH\cdot DB=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(DH\cdot DB=AH\cdot AM\)
31 tháng 10 2023
a: ΔABD vuông tại A
=>\(BD^2=AB^2+AD^2\)
=>\(BD^2=9^2+12^2=225\)
=>BD=15(cm)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot15=12\cdot9=108\)
=>AH=108/15=7,2(cm)
XétΔABD vuông tại A có \(sinBDA=\dfrac{AB}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\)
nên \(\widehat{BDA}\simeq37^0\)
b: Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(1\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\left(2\right)\)
Từ (1) và (2) suy ra \(AI\cdot AB=HD\cdot HB\)
c: Xét ΔHDN vuông tại H và ΔHMB vuông tại H có
\(\widehat{HDN}=\widehat{HMB}\left(=90^0-\widehat{DBC}\right)\)
Do đó: ΔHDN đồng dạng với ΔHMB
=>HD/HM=HN/HB
=>\(HM\cdot HN=HD\cdot HB=HA^2\)
BH
1
8 tháng 10 2019
hình bạn tự vẽ nha
áp dụng định lý py ta go vào tam giác ABD ta có AD^2 + AB^2 =64 (1)
áp dụng định lý pytago vào tam giác ABH ta có AB^2 = AH^2+ 36 (2)
áp dụng định lý pytago vào tam giác AHD ta có AD^2= AH^2 +4 (3)
thay (2)và (3) vào (1)
ta có 2AH^2 =24
=> AH^2 =12
thay AH^2=12 lần lượt vào 2 và 3
=> AB^2=12+36=48=>AB=\(\sqrt{48}\)
AD^2=12+4=16 => AD=4
29 tháng 5 2022
Áp dụng định lý pitago: \(AC=\sqrt{12^2+9^2}=\sqrt{225}=15\left(cm\right)\)
Xét tam giác HBA và tam giác ABC, có:
\(\widehat{BHA}=\widehat{ABC}=90^o\)
\(\widehat{A}\): chung
Vậy tam giác HAB đồng dạng tam giác BAC ( g.g )
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AB}{AC}=\dfrac{HB}{BC}\)
\(\Rightarrow AH=\dfrac{AB^2}{AC}=\dfrac{12^2}{15}=9,6\left(cm\right)\)
\(\Rightarrow HB=\dfrac{AB.BC}{AC}=\dfrac{12.9}{15}=7,2\left(cm\right)\)
\(S_{AHB}=\dfrac{1}{2}.AH.HB=\dfrac{1}{2}.9,6.7,2=34,56\left(cm^2\right)\)
29 tháng 5 2022
a,
Xét Δ HBA và Δ BAC, có :
\(\widehat{BHA}=\widehat{ABC}=90^o\)
\(\widehat{ABH}=\widehat{CAB}\) (cùng phụ \(\widehat{ABC}\))
=> Δ HBA ~ Δ BAC (g.g)