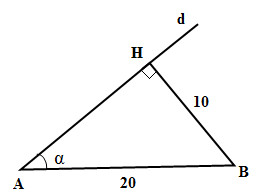
Mọi người ơi cho mình hỏi cách chứng minh đỉnh của (P) luôn thuộc một đường thẳng cố định ta làm thế nào vậy??
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2021
TL
Hình dung được sự thay đổi của điểm di động và các điểm có liên quan với nó thay đổi như thế nào.
Xem xét các đại lượng không đổi, các điểm không thay đổi khi ta cho điểm di động di chuyển.
Chứng minh điểm đó là điểm cố định vì nó là điểm đặc biệt nào đó của đoạn thẳng , hoặc đường tròn cố định nào đó.
HT
CM
6 tháng 8 2019
Chứng minh họ đường thẳng y = mx + (2m + 1) (1) luôn đi qua một điểm cố định nào đó.
Giả sử điểm A( x o ; y o ) là điểm mà họ đường thẳng (1) đi qua với mọi m. Khi đó tọa độ điểm A nghiệm đúng phương trình hàm số (1).
Với mọi m, ta có: y o = m x o + (2m + 1) ⇔ ( x o + 2)m + (1 – y) = 0
Vì phương trình nghiệm đúng với mọi giá trị của m nên tất cả các hệ số phải bằng 0.
Suy ra: x o + 2 = 0 ⇔ x o = -2
1 – y o = 0 ⇔ y o = 1
Vậy A(-2; 1) là điểm cố định mà họ đường thẳng y = mx + (2m + 1) luôn đi qua với mọi giá trị m.
1 tháng 5 2017
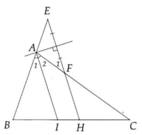
Gọi h (AH) là đường cao của \(\Delta ABC\) thì h là hằng số không đổi và cạnh đáy BC bằng a cố định .
Ta có : \(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}a.h\) không đổi .
Vậy diện tích tam giác ABC luôn không đồi nếu có đáy BC cố định và đỉnh A di động trên 1 đường thẳng d cố định song song với đường thẳng BC .
8 tháng 12 2019
sắp thi rồi mà vẫn chưa bt nữa hả ????????????????????????????????????????????????????????????
thêm 0 vào khi chia số tp
8 tháng 12 2019
Time Power
TH em nói là TH nào
nếu thêm 0 thì nhiều TH lắm :))