cho nửa đường tròn O đường kính AB và dây EF ko cắt AB . I và K lần lượt là chân các đườg vuông góc kẻ từ A B đến EF . chứng minh diện tích IKBA bằg tổng diện tích tam giác AEB và BFA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 11 2017
bạn ơi cho mình hỏi bước thứ nhất bạn làm theo định lí gì v bạn
CM
9 tháng 10 2017
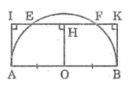
Ta có: AI ⊥ EF (gt)
BK ⊥ EF (gt)
Suy ra: AI // BK
Suy ra tứ giác ABKI là hình thang
Kẻ OH ⊥ EF
Suy ra: OH // AI // BK
Ta có: OA = OB (= R)
Suy ra: HI = HK
Hay: HE + EI = HF + FK (1)
Lại có: HE = HF (đường kính dây cung) (2)
Từ (1) và (2) suy ra: IE = KF
DT
15 tháng 2 2022
cho mình lm vs đề nửa đường tròn hén :
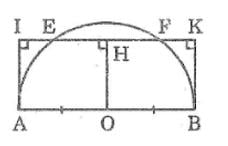
bn tk hình thay K là J thì nó cũng là hình đúm nuôn
Ta có : \(AI\perp EF\)(gt)
\(BJ\perp EF\left(gt\right)\)
=> AI//BJ
Suy ra tứ giác ABJI là hình thang
Kẻ OH ⊥ EF
Suy ra: OH // AI // BJ
Ta có: OA = OB (= R)
Suy ra: HI = HJ
Hay: HE + EI = HF + FJ (1)
Lại có: HE = HF (đường kính dây cung) (2)
Từ (1) và (2) suy ra: IE = JF
CM
26 tháng 9 2017
Gọi G là giao điểm của AH và EF
Tứ giác AEHF là hình chữ nhật => AH = EF
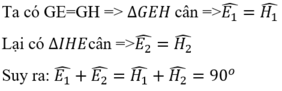
Do đó EF là tiếp tuyến của đường tròn (I)
Tương tự, EF là tiếp tuyến của đường tròn (K)
TN
9 tháng 8 2016
gọi O là tâm đường tròn đường kính AB
Kẻ OE vuông góc vs CD (E thuộc CD)
suy ra E là trung điểm của CD
Mà OE là đường trung bình của hình thang ABKH (đi qua trung điểm một cạnh bên và song song vs cạnh đáy)
suy ra EH=EK mà EC=ED Suy ra đpcm