Tính giá trị biểu thức:
A = x2 - y2 + 2x + 1 tại x = 6,5, y = 2,5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A=x^2-4=\left(x-2\right)\left(x+2\right)\)
Khi x=102 thì \(A=\left(102-2\right)\left(102+2\right)=104\cdot100=10400\)
b: \(B=x^2+6x+9=x^2+2\cdot x\cdot3+3^2=\left(x+3\right)^2\)
Khi x=997 thì \(B=\left(997+3\right)^2=1000^2=1000000\)
c: \(C=4x^2-4xy+y^2=\left(2x\right)^2-2\cdot2x\cdot y+y^2=\left(2x-y\right)^2\)
Khi x=39 và y=-2 thì \(C=\left(2\cdot39+2\right)^2=80^2=6400\)

\(a,=5\left(x^2+2xy+y^2\right)-10y^2+5=5\left(x+y\right)^2-10y^2+5\\ =5\left(1+2\right)^2-10\cdot4+5=45-40+5=10\\ b,=7\left(x-y\right)-\left(x-y\right)^2=\left(x-y\right)\left(7-x+y\right)\\ =\left(2-2\right)\left(7-2+2\right)=0\)
b: \(=7\left(x-y\right)-\left(x-y\right)^2\)
\(=\left(x-y\right)\left(7-x+y\right)=0\)

a)A=(2x+3y)(x2-xy+1)-x2(2x-y)-3x tại x=-1;y=2
Rút gọn:
A = 2x3 - 2x2y + 2x + 3x2y - 3xy2+ 3y - 2x3 + x2y - 3x (phá ngoặc)
=> A = 2x2y - 3xy2 - x + 3y
Thay x = -1 và y = 2; ta được:
A = 23
b)B=2xy.(1/4x2-3y)+5y(xy-x3+1) tại x=1;y=1/2
B = x3y/2 - 6xy2 + 5xy2 - 5x3y + 5y (phá ngoặc)
B = -9x3y/10 - xy2 + 5y
Thay x = 1 và y = 1/2 ta được:
B = 0
Bài này tuy có hơi cồng kềnh chút nhưng chỉ cần em chịu khó phá ngoặc là sẽ giải quyết được nhé!

a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)

a: \(A=x^2+y^2=\left(x+y\right)^2-2xy=15^2-2\cdot50=115\)
c: \(x-y=\sqrt{\left(x+y\right)^2-4xy}=\sqrt{15^2-4\cdot50}=5\)
\(C=x^2-y^2=\left(x+y\right)\left(x-y\right)=15\cdot5=75\)

Ta có: \(\left\{{}\begin{matrix}x^2+2y+1=0\\y^2+2z+1=0\\z^2+2x+1=0\end{matrix}\right.\)
\(\Rightarrow x^2+2y+1+y^2+2z+1+z^2+2x+1=0\)
\(\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2+\left(z+1\right)^2=0\)
\(\Rightarrow x=y=z=-1\)(do \(\left(x+1\right)^2,\left(y+1\right)^2,\left(z+1\right)^2\ge0\forall x,y,z\))
a) \(A=x^{2020}+y^{2020}+z^{2020}=\left(-1\right)^{2020}+\left(-1\right)^{2020}+\left(-1\right)^{2020}=1+1+1=3\)
b) \(B=\dfrac{1}{x^{2020}}+\dfrac{1}{y^{2020}}+\dfrac{1}{z^{2020}}=\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}=\dfrac{1}{1}+\dfrac{1}{1}+\dfrac{1}{1}=3\)
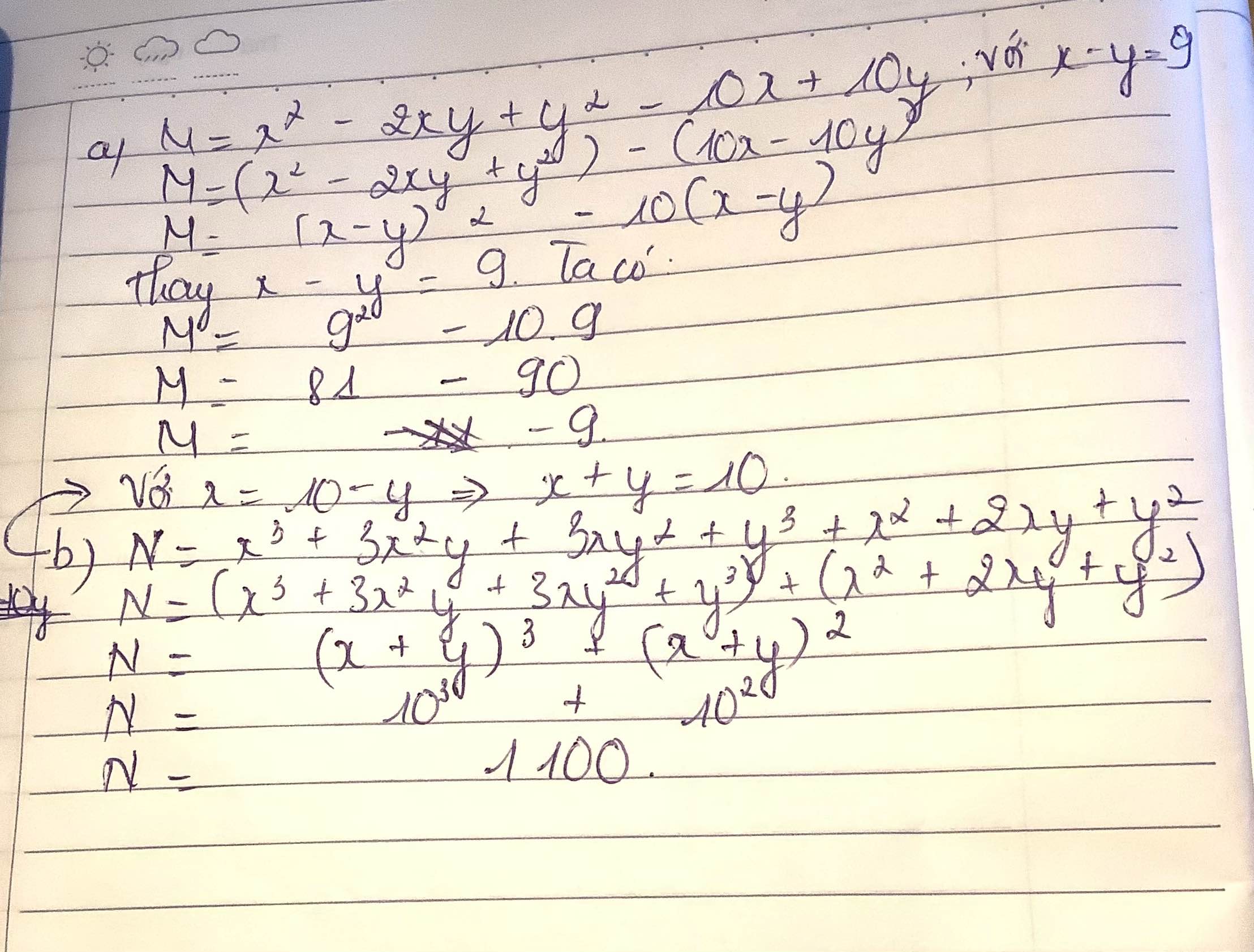
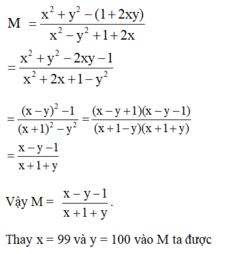
A = x2 + 2x + 1 - y2
= (x + 1)2 - y2
= (x + 1 - y) (x + 1 + y)
Với x = 6,5, y = 2,5, ta có:
= (6,5 + 1 - 2,5) (6,5 + 1 + 2,5)
= 5 . 10 = 50
Vậy khi x = 6,5, y = 2,5 thì A = 50.