Chứng minh
CotA+cotB+cotC=AB2+AC2+ BC2/4.S
Mik cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2019
Chỉ đúng với điều kiện A, B, C là 3 góc trong tam giác \(\Rightarrow A+B+C=\pi\)
Đặt \(\frac{A}{2}=x\) , \(\frac{B}{2}=y\); \(\frac{C}{2}=z\) \(\Rightarrow x+y+z=\frac{\pi}{2}\Rightarrow\left\{{}\begin{matrix}x+y=\frac{\pi}{2}-z\\z=\frac{\pi}{2}-\left(x+y\right)\end{matrix}\right.\)
\(cot\frac{A}{2}+cot\frac{B}{2}+cot\frac{C}{2}=cotx+coty+cotz=\frac{cosx}{sinx}+\frac{cosy}{siny}+\frac{cosz}{sinz}\)
\(=\frac{cosx.siny+cosy.sinx}{sinx.siny}+\frac{cosz}{sinz}=\frac{sin\left(x+y\right)}{sinx.siny}+\frac{cosz}{sinz}\)
\(=\frac{sin\left(\frac{\pi}{2}-z\right)}{sinx.siny}+\frac{cosz}{sinz}=\frac{cosz}{sinx.siny}+\frac{cosz}{sinz}=cosz\left(\frac{1}{sinx.siny}+\frac{1}{sinz}\right)\)
\(=\frac{cosz}{sinx.siny.sinz}\left(sinz+sinx.siny\right)=\frac{cosz}{sinx.siny.sinz}\left(sin\left(\frac{\pi}{2}-\left(x+y\right)\right)+sinxsiny\right)\)
\(=\frac{cosz}{sinx.siny.sinz}\left(cos\left(x+y\right)+sinx.siny\right)\)
\(=\frac{cosz}{sinx.siny.sinz}\left(cosx.cosy-sinx.siny+sinx.siny\right)\)
\(=\frac{cosx.cosy.cosz}{sinx.siny.sinz}=cotx.coty.cotz=cot\frac{A}{2}.cot\frac{B}{2}.cot\frac{C}{2}\)
ST
0
P
1
13 tháng 3 2022
Câu 20: Tam giác ABC vuông tại B suy ra:
A. AC2 = AB2 + BC2 B. AC2 = AB2 - BC2
C. BC2 = AB2 + AC2 D. AB2 = BC2 + AC2
Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?
A. Tại B B. Tại C
C. Tại A D. Không phải là tam giác vuông
Câu 22: Cho ABC có = 900 ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:
A. 6,5 cm B. 5,5 cm C. 6 cm D. 6,2 cm
Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:
A. 3cm, 4dm, 5cm. B. 5cm, 14cm, 12cm.
C. 5cm, 5cm, 8cm. D. 9cm, 15cm, 12cm.
Câu 24: Cho ABC có AB = AC và = 600, khi đó tam giác ABC là:
A. Tam giác vuông B. Tam giác cân
C. Tam giác đều D. Tam giác vuông cân
Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:
A. ∠A ≤ 900 B. ∠A > 900 C. ∠A < 900 D. ∠A = 900
vuông tại B chọn câu đúng
PT
1
CM
27 tháng 11 2018
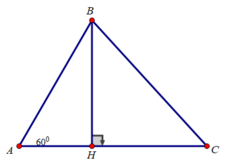
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
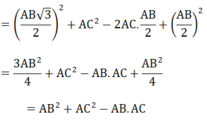
Vậy được điều phải chứng minh.
PT
1
CM
16 tháng 12 2018
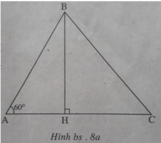
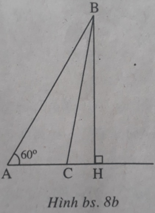
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60 ° là góc nhọn), do đó H C 2 = A C - A H 2 (xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2 = B H 2 + A C 2 + A H 2 - 2 A C . A H = A B 2 + A C 2 - 2 A C . A H
Do ∠ (BAC) = 60 ° nên AH = AB.cos 60 ° = AB/2, suy ra B C 2 = A B 2 + A C 2 - A B . A C