Minh và Nam đứng ở hai đểm M , N cách nhau 750m trên một bãi sông. Khoảng cách từ M đến sông 150m từ N đến sông 600m. Tính thời gan ngắn nhất để Minh hạy ra sông múc một thùng nước mang đến chỗ Nam . Cho biết đoạn sông thẳng , vận tốc chạy của Minh không đổi v= 2m/s , bỏ qua thời gian múc nước
vẽ sơ đồ chuyển động



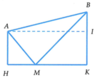
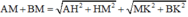
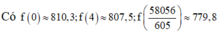

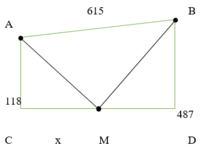
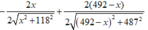
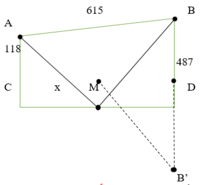
Giả sử Minh và Nam đi theo đường MI'N . Gọi điểm N' là điểm đối xứng N qua bãi sông.
Ta có : MI'N = MI' + I'N = MI' + I'N' = MI'N'
Để MI'N ngắn nhất thì ba điểm M;I';N' thẳng hàng. Lúc đó I = I'
=> NP = NK - PK = NK - NH = 450 (m)
\(MP=\sqrt{MN^2-NP^2}=600\left(m\right)\)
N'P = N'K + KP = 750 (m)
\(MN'=\sqrt{MP^2+N'P^2}=150\sqrt{41}\left(m\right)\)
Thời gian ngắn nhất là :
\(t=\frac{MN'}{V}=\frac{150\sqrt{41}}{2}=75\sqrt{41}=480\left(s\right)=8\left(phút\right)\)
Giả sử Minh và Nam đi theo đường MI'N . Gọi điểm N' là điểm đối xứng N qua bãi sông.
Ta có : MI'N = MI' + I'N = MI' + I'N' = MI'N'
Để MI'N ngắn nhất thì ba điểm M;I';N' thẳng hàng. Lúc đó I = I'
=> NP = NK - PK = NK - NH = 450 (m)
MP=√MN2−NP2=600(m)
N'P = N'K + KP = 750 (m)
MN'=√MP2+N'P2=150√41(m)
Thời gian ngắn nhất là :
t=MN'V =150√412 =75√41=480(s)=8(phút)