Tìm x,y biết :
x2+x=y4+y3+y2+y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
AH
Akai Haruma
Giáo viên
29 tháng 12 2023
Lời giải:
$x^3+y^3=(x+y)^3-3xy(x+y)=2^3-3xy.2=8-6xy$
$=8-3.2xy=8-3[(x+y)^2-(x^2+y^2)]=8-3(2^2-34)=98$
----------------
$x^4+y^4=(x^2+y^2)^2-2x^2y^2=34^2-\frac{1}{2}(2xy)^2$
$=34^2-\frac{1}{2}[(x+y)^2-(x^2+y^2)]^2=34^2-\frac{1}{2}(2^2-34)^2=706$
4 tháng 9 2021
a: Ta có: \(\left(x+y\right)^2\)
\(=x^2+2xy+y^2\)
\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)
CM
11 tháng 2 2018
Ta có: VT = ( x 3 + x 2 y + x y 2 + y 3 )(x - y)
= ( x- y). ( x 3 + x 2 y + x y 2 + y 3 ).
= x. ( x 3 + x 2 y + x y 2 + y 3 ) - y( x 3 + x 2 y + x y 2 + y 3 )
= x 4 + x 3 y + x 2 y 2 + x y 3 – x 3 y – x 2 y 2 – x y 3 – y 4
= x 4 – y 4 = VP (đpcm)
Vế trái bằng vế phải nên đẳng thức được chứng minh.
CM
22 tháng 8 2019
Ta có :
y và x là hai đại lượng tỉ lệ nghịch với nhau ⇒ y = a/x
Nên hệ số tỉ lệ a = x.y = 2.30 = 60
CM
19 tháng 8 2018
Theo đề bài ta có :
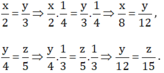
Do đó ta có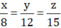 
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
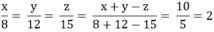
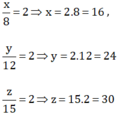
Vậy x =16 ; y = 24 ; z =30
AH
Akai Haruma
Giáo viên
11 tháng 7 2021
Lời giải:
a.
$x^3+y^3=(x+y)^3-3xy(x+y)=9^3-3.9.18=243$
$x^4+y^4=(x^2+y^2)^2-2x^2y^2=[(x+y)^2-2xy]^2-2x^2y^2$
$=[9^2-2.18]^2-2.18^2=1377$
Nếu $x\geq y$ thì:
$x^3-y^3=(x-y)(x^2+xy+y^2)$
$=|x-y|[(x+y)^2-xy]=\sqrt{(x+y)^2-4xy}[(x+y)^2-xy]$
$=\sqrt{9^2-4.18}(9^2-18)=189$
Nếu $x< y$ thì $x^3-y^3=-189$
b.
$A=(x+y)^2-6(x+y)+y-5$
$=(-9)^2-6(-9)+y-5=130+y$
Chưa đủ cơ sở để tính biểu thức.
3 tháng 10 2023
`#3107.101107`
`D = x^3 - y^3 - 3xy` biết `x - y - 1 = 0`
Ta có:
`x - y - 1 = 0`
`=> x - y = 1`
`D = x^3 - y^3 - 3xy`
`= (x - y)(x^2 + xy + y^2) - 3xy`
`= 1 * (x^2 + xy + y^2) - 3xy`
`= x^2+ xy + y^2 - 3xy`
`= x^2 - 2xy + y^2`
`= x^2 - 2*x*y + y^2`
`= (x - y)^2`
`= 1^2 = 1`
Vậy, với `x - y = 1` thì `D = 1`
________
`E = x^3 + y^3` với `x + y = 5; x^2 + y^2 = 17`
`x + y = 5`
`=> (x + y)^2 = 25`
`=> x^2 + 2xy + y^2 = 25`
`=> 2xy = 25 - (x^2 + y^2)`
`=> 2xy = 25 - 17`
`=> 2xy = 8`
`=> xy = 4`
Ta có:
`E = x^3 + y^3`
`= (x + y)(x^2 - xy + y^2)`
`= 5 * [ (x^2 + y^2) - xy]`
`= 5 * (17 - 4)`
`= 5 * 13`
`= 65`
Vậy, với `x + y = 5; x^2 + y^2 = 17` thì `E = 65`
________
`F = x^3 - y^3` với `x - y = 4; x^2 + y^2 = 26`
Ta có:
`x - y = 4`
`=> (x - y)^2 = 16`
`=> x^2 - 2xy + y^2 = 16`
`=> (x^2 + y^2) - 2xy = 16`
`=> 2xy = (x^2 + y^2) - 16`
`=> 2xy = 26 - 16`
`=> 2xy = 10`
`=> xy = 5`
Ta có:
`F = x^3 - y^3`
`= (x - y)(x^2 + xy + y^2)`
`= 4 * [ (x^2 + y^2) + xy]`
`= 4 * (26 + 5)`
`= 4*31`
`= 124`
Vậy, với `x - y = 4; x^2 + y^2 = 26` thì `F = 124.`
3 tháng 8 2023
a) \(\left(x-5\right)^2=\left(3+2x\right)^2\)
\(\Rightarrow\left(3+2x\right)^2-\left(x-5\right)^2=0\)
\(\Rightarrow\left(3+2x+x-5\right)\left(3+2x-x+5\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(x+8\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}3x-2=0\\x+8=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-8\end{matrix}\right.\)
b) \(27x^3-54x^2+36x=9\)
\(\Rightarrow27x^3-54x^2+36x-9=0\)
\(\Rightarrow27x^3-54x^2+36x-8+8-9=0\)
\(\Rightarrow\left(3x-2\right)^3-1=0\)
\(\Rightarrow\left(3x-2-1\right)\left[\left(3x-2\right)^2+3x-2+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2\right)^2+3x-2+\dfrac{1}{4}-\dfrac{1}{4}+1\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-2+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]=0\)
\(\Rightarrow\left(3x-3\right)\left[\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\right]=0\left(1\right)\)
mà \(\left(3x-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0,\forall x\)
\(\left(1\right)\Rightarrow3x-3=0\Rightarrow3x=3\Rightarrow x=1\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 8 2023
(\(x-5\))2 = (3 +2\(x\))2 ⇒ \(\left[{}\begin{matrix}x-5=3+2x\\x-5=-3-2x\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=-8\\x=\dfrac{2}{3}\end{matrix}\right.\) vậy \(x\in\){-8; \(\dfrac{2}{3}\)}
27\(x^3\) - 54\(x^2\) + 36\(x\) = 9
27\(x^3\) - 54\(x^2\) + 36\(x\) - 8 = 1
(3\(x\) - 2)3 = 1 ⇒ 3\(x\) - 2 = 1 ⇒ \(x\) = 1