tìm n thuộc Nđể các phép chia sau là phép chia hết
a,3xnyz:4x2y
b,5xn+1:2x3
cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
1
AH
Akai Haruma
Giáo viên
9 tháng 9 2021
Lời giải:
$2x^3-x^2+4=2x^2(x+1)-3x(x+1)+3(x+1)+1$
$=(x+1)(2x^2-3x+3)+1$
Với $x$ nguyên, để $2x^3-x^2+4\vdots x+1$ thì $1\vdots x+1$
$\Rightarrow x+1\in \text{Ư(1)}$
$\Rightarrow x+1\in\left\{\pm 1\right\}$
$\Rightarrow x\in\left\{-2; 0\right\}$
PT
1
CM
1 tháng 12 2017
x n y n + 1 : x 2 y 5 = x n : x 2 y n + 1 : y 5 = x n - 2 . y n - 4 là phép chia hết
16 tháng 8 2023
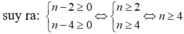
a) \(35x^9y^n=5.\left(7x^9y^n\right)\)
Để \(35x^9y^n⋮\left(-7x^7y^2\right)\)
\(\Rightarrow n\in\left\{0;1;2\right\}\)
16 tháng 8 2023
b) \(5x^3-7x^2+x=3x\left(\dfrac{5}{3}x^2-\dfrac{7}{3}x+\dfrac{1}{3}\right)\)
Để \(\left(5x^3-7x^2+x\right)⋮3x^n\)
\(\Rightarrow3x\left(\dfrac{5}{3}x^2-\dfrac{7}{3}x+\dfrac{1}{3}\right)⋮3x^n\)
\(\Rightarrow n\in\left\{0;1\right\}\)
PT
1
CM
27 tháng 5 2018
Vì x 5 - 2 x 3 - x chia hết cho 7xn nên mỗi hạng tử của đa thức chia hết cho 7 x n
Suy ra: x chia hết cho 7 x n ( trong đó x là hạng tử có số mũ nhỏ nhất).
Nên n ≤ 1
Vì n ∈ N ⇒ n = 0 hoặc n = 1
Vậy n = 0 hoặc n = 1 thì x 5 - 2 x 3 - x : 7 x n
CM
18 tháng 1 2018
Vì 5 x 5 y 5 - 2 x 3 y 3 - x 2 y 2 chia hết cho 2 x n y n nên mỗi hạng tử của đa thức đều chia hết cho 2 x n y n
Suy ra: x 2 y 2 chia hết cho 2 x n y n trong đó x 2 y 2 là hạng tử có số mũ nhỏ nhất).
Suy ra: n ≤ 2
Vì n ∈ N ⇒ n = 0; n = 1; n = 2
Vậy với n ∈ {0; 1; 2} thì 5 x 5 y 5 - 2 x 3 y 3 - x 2 y 2 : 2 x n y n