Cho tam giác ABC vuông tại A, đường cao AH. Biết AC=15cm, AB=20cm. Tính BC, AH và chu vi tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
22 tháng 7 2018
BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= 
= 
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= 
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:
· 
KT
22 tháng 7 2018
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)
21 tháng 7 2023
1: AB/AC=5/7
=>HB/HC=(AB/AC)^2=25/49
=>HB/25=HC/49=k
=>HB=25k; HC=49k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>1225k^2=15^2=225
=>k^2=9/49
=>k=3/7
=>HB=75/7cm; HC=21(cm)
24 tháng 3 2021
Áp dụng định lý \(Pi-ta -go \) và tam giác vuông \(ABC\) ta có :
\(AB^2+AC^2=BC^2\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(=\sqrt{20^2+25^2}=5\sqrt{41}\) \(\left(cm\right)\)
Chu vi \(\Delta ABC\) là :\(AB+AC+BC=20+25+5\sqrt{41}=45+5\sqrt{41}\left(cm\right)\)
12 tháng 7 2023
1:
BC=15+20=35cm
AD là phân gíac
=>AB/BD=AC/CD
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=35^2
=>k=7
=>AB=21cm; AC=28cm
AH=21*28/35=16,8cm
\(AD=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)
2:
BC=căn 12^2+16^2=20cm
HB=AB^2/BC=12^2/20=7,2cm
HC=20-7,2=12,8cm
TL
2
4 tháng 10 2021
Áp dụng Pytago \(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9\left(cm\right)\\AH=\dfrac{15\cdot20}{25}=12\left(cm\right)\end{matrix}\right.\)
16 tháng 12 2023
a: Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>\(BC=\sqrt{625}=25\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>\(AH=\dfrac{300}{25}=12\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(4\right)\)
Từ (3) và (4) suy ra \(AM\cdot AB=AN\cdot AC\)
=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
Do đó: ΔAMN đồng dạng với ΔACB
c: Ta có: ΔABC vuông tại A
mà AK là đường trung tuyến
nên AK=KC=KB
Ta có: KA=KC
=>ΔKAC cân tại K
=>\(\widehat{KAC}=\widehat{KCA}\)
Ta có: ΔAMN đồng dạng với ΔACB
=>\(\widehat{ANM}=\widehat{ABC}\)
Ta có: \(\widehat{KAC}+\widehat{ANM}\)
\(=\widehat{ABC}+\widehat{KCA}=90^0\)
=>AK\(\perp\)MN tại I
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2;CH\cdot BC=CA^2\)
=>\(BH\cdot25=15^2=225;CH\cdot25=20^2=400\)
=>BH=225/25=9(cm); CH=400/25=16(cm)
Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\)
=>\(AM\cdot15=12^2\)=144
=>AM=144/15=9,6(cm)
Ta có: AMHN là hình chữ nhật
=>AH=MN
mà AH=12cm
nênMN=12cm
Ta có: ΔANM vuông tại A
=>\(AN^2+AM^2=NM^2\)
=>\(AN^2+9,6^2=12^2\)
=>AN=7,2(cm)
Xét ΔIMA vuông tại I và ΔAMN vuông tại A có
\(\widehat{IMA}\) chung
Do đó: ΔIMA đồng dạng với ΔAMN
=>\(\dfrac{S_{IMA}}{S_{AMN}}=\left(\dfrac{AM}{MN}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)
=>\(S_{IMA}=\dfrac{16}{25}\cdot\dfrac{1}{2}\cdot AM\cdot AN=22,1184\left(cm^2\right)\)
13 tháng 6 2021
a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)
\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)
* Áp dụng hệ thức :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)
\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)
\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm
\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm
\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)
Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm2
13 tháng 6 2021
b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Lại có : \(BC=BD+DC=15+20=35\)cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)
\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm
\(\Rightarrow AB=\frac{3}{4}.28=21\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm
\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm
Áp dụng định lí Pytago cho tam giác AHD vuông tại H
\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm
DT
24 tháng 5 2022
a ) .
Xét 2 t/g vuông : ABC và HBA có:
góc B chung
do đó:
t/g ABC đồng dạng t/g HBA ( g - g )
b ) .
Áp dụng đl pytao vào t/g vuông ABC có :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\left(cm\right)\)
vi t/g ABC đồng dạng t/g HBA
=> \(\dfrac{AC}{HA}=\dfrac{BC}{AB}\Leftrightarrow\dfrac{20}{HA}=\dfrac{25}{15}\Rightarrow HA=20:\dfrac{25}{15}=12\left(cm\right)\)
30 tháng 9 2021
bài 9
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=152+202=625
BC=25cm
* AH.BC=AB.AC
AH.25=15.20
AH.25=300
AH=12cm
30 tháng 9 2021
tam giác ABH vuông tại H có
BH2=AB2-AH2
BH2=152-122=81
BH=9cm
tam giác ABC vuông tại A có
*AB2=BH.BC
225=9.BC
BC=25cm
CH=BC-BH=25-9=16cm
*AC2=BC2-AB2
AC2=252-152=400
AC=20cm
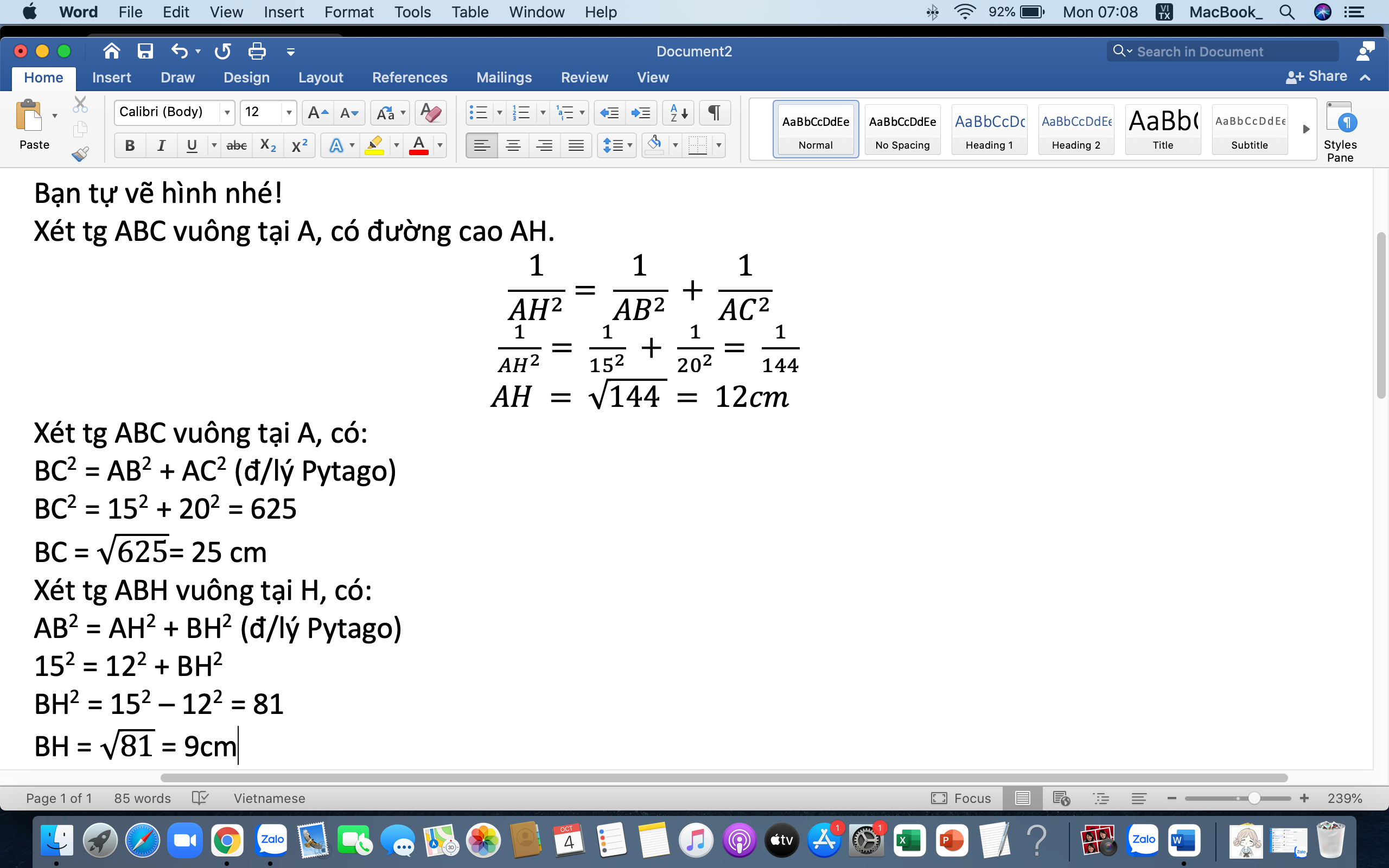
Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{20^2+15^2}=25\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)
Ta có: \(P_{ABC}=AB+AC+BC=20+15+25=60\left(cm\right)\)