Cho hình bình hành ABCD.E,F lần lượt là trung điểm của AB,AD.CE và CF lần lượt cắt BD tai M,N.Chứng minh rằng DM=MN=NB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 9 2021
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Xét ΔDNC có
F là trung điểm của DC
FM//NC
Do đó: M là trung điểm của DN
Suy ra: DM=MN(1)
Xét ΔABM có
E là trung điểm của AB
EN//AM
Do đó: N là trung điểm của BM
Suy ra: BN=NM(2)
Từ (1) và (2) suy ra DM=MN=NB
CM
19 tháng 12 2017
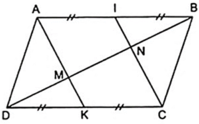
Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có: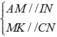
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
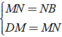⇒ DM = MN = NB
MN
27 tháng 8 2021
AECF là hình bình hành => EN // AM
E là trung điểm của AB => N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy →DM=→MN=→NB
LL
28 tháng 10 2017
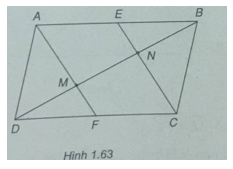
xét tứ giác AECF: có AE = FC và AE//FC => AECF là hình bình hành => AF//CE
xét △DNC: có F là trung điểm của DC và FM//CN (đường tb) => M là trung điểm của DN => vtDM = vtMN (1)
xét △BMA: có E là trung điểm của AB và NE//AM ( đường tb) => N là trung điểm của MB => BM=MN (2)
từ (1) và (2) suy ra : DM=MN=NB => vtDM = vtMN = vtNB ( cùng hướng, cùng độ lớn)
14 tháng 7 2018
a)
Vì \(DC=AB\)(vì ABCD là hình bình hành) (1)
mà \(IC=ID\) (2)
\(KA=KB\)(3)
Từ (1) ;/ (2) và (3)
\(\Rightarrow IC=KB\)
Vì ABCD là hình b/hành
\(\Rightarrow AD=BC\)
và \(\widehat{ADI}=\widehat{CBK}\)
Xét \(\Delta ADI\)và \(\Delta CBK\)có :
\(AD=BC\left(cmt\right)\)
\(\widehat{ADI}=\widehat{CBK}\left(cmt\right)\)
\(DI=BK\)(cmt )
Do đó : \(\Delta ADI=\Delta CBK\)(c-g-c)
\(\Rightarrow\hept{\begin{cases}AI=CK\\\widehat{DAI}=\widehat{BCK}\end{cases}}\)
Mà \(\widehat{DAB}=\widehat{DCB}\)( vì ABCD Là hình bình hành )
\(\Rightarrow\widehat{IAB}=\widehat{ICK}\)
Mà hai góc này ở vị trí so le
\(\Rightarrow AI//CK\)
b) Xét \(\Delta MAB\)có :
\(KA=KB\left(gt\right)\)
và \(AM//KN\)(vì AI // KC )
=> MN= NB ( 1)
Xét \(\Delta CDN\)có :
\(ID=IC\left(gt\right)\)
và \(IM//CN\)(vì IA // CK )
=> DM = MN (2)
Từ (1) và (2)
\(\Rightarrow DM=MN=NB\)( đpcm)
28 tháng 2 2022
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét ΔAEM có
E là trung điểm của AB
EN//AM
Do đó; N là trung điểm của BM
=>BN=NM(1)
Xét ΔDNC có
F là trung điểm của DC
FM//NC
Do đó: M là trung điểm của DN
=>DM=MN(2)
Từ (1) và (2) suy ra DM=MN=NB
c: Xét ΔADM và ΔCBN có
AD=CB
\(\widehat{ADM}=\widehat{CBN}\)
DM=BN
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN
mà EN=AM/2
và MF=CN/2
nên EN=MF
Xét tứ giác MENF có
NE//MF
NE=MF
Do đó: MENF là hình bình hành
8 tháng 12 2014
Bạn tự vẽ hình nha ^^
a) Ta có: AB=CD (gt), mà E,F lần lượt và trung điểm của AB và CD.
=> EA=EB=FD=FC
Ta có: AB song song => EA song song FC
Ta có EA=FC và EA song song FC
=> AECF là hình bình hành.
Tương tự chứng minh BEDF là hình bình hành.
b) Kẻ EF.
Ta có: EA=FD (cmt); AB song song CD => EA song song FD
=> AEFD là hình bình hành
Tương tự chứng minh EBCF là hình hình hành.
Ta có: E là trung điểm AB
K là trung điểm của BF (hai đường chéo EC và BF của hình bình hành cắt nhau tại trung điểm mỗi đường)
=> KE là đường trung bình của tam giác ABF
=> KE song song AF và KE=1/2 AF (1)
Ta có hai đường chéo AF và DE của hình bình hành AEFD => I là trung điểm của AF => IF=1/2 AF (2)
Từ (1) và (2) suy ra IF=KE và KE song song AF
=> EIFK là hình bình hành
c) Xét hình bình hành ABCD có AC và BD là hai đường chéo => AC và BD cắt nhau tại trung điểm mỗi đường (1)
Xét hình bình hành AEFC có hai đường chéo là EF và AC => EF và AC cắt nhau tại trung điểm mỗi đường (2)
Từ (1) và (2) suy ra AC, BD, EF cùng đi qua một diểm.
d) Giả sử EIFK là hình vuông.
=> IF = IE
Mà IF=IA, IE=ID (hai đường chéo AF và DE cắt nhau tại trung điểm mỗi đường)
=> IE=ID=IA=IF
=> AF=DE
Hình bình hành AEFD có hai đường chéo bằng nhau => là hình chữ nhật.
=> DAE= 90 độ
Ta có hình bình hành ABCD có một góc vuông => là hình chữ nhật.
Vậy để EIFK là hình vuông thì ABCD phải là hình chữ nhật.
e) Gọi giao điểm của AC và DB là O
Ta có DO là đường trung tuyến xuất phát từ đỉnh D của tam giác DAC
AF là đường trung tuyến xuất phát từ đỉnh A của tam giác DAC
DO và AF cắt nhau tại M
=> M là trọng tâm của tam giác DAC
=> DM=2/3 DO, MO=1/3 DO (1)
Tương tự chứng minh NB=2/3 BO và NO=1/3 BO (2)
Ta có OB=OD (3)
Từ (1), (2) và (3) suy ra DM=NB
Ta có MN=MO+NO=1/3 DO+ 1/3 BO= 2/3 DO = 2/3 BO
=> DM=MN=NB