Cho đường tròn tâm O, đường kính AB. Ke dây cung CD (C thuộc cung AD). AC cắt BD tại M , AD cắt BC tại H.
a, Chứng minh : H là trực tâm của tam giác MAB.
MH cắt AB tại K.Chứng minh 4 điểm K, H, D, B thuộc một đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC
a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC

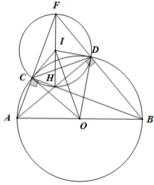
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B

a) Ta có: \(\widehat{AMO}=\widehat{ADO}=\widehat{ANO}=90^o\) nên \(M,N,D\) cùng nhìn \(AO\) dưới một góc vuông suy ra \(M,D,O,N,A\) cùng thuộc một đường tròn.
b) Gọi \(F\) là giao điểm của \(AC\) và đường tròn \(\left(O\right)\).
\(\Delta ANF\sim\Delta ACN\left(g.g\right)\) suy ra \(AN^2=AC.AF\).
Xét tam giác \(AHN\) và tam giác \(AND\):
\(\widehat{HAN}=\widehat{NAD}\) (góc chung)
\(\widehat{ANH}=\widehat{ADN}\) (vì \(AMDON\) nội tiếp, \(\widehat{ANH},\widehat{ADN}\) chắn hai cung \(\stackrel\frown{AM},\stackrel\frown{AN}\) mà \(AM=AN\))
\(\Rightarrow\Delta AHN\sim\Delta AND\left(g.g\right)\)
suy ra \(AN^2=AH.AD\)
suy ra \(AC.AF=AH.AD\)
\(\Rightarrow\Delta AFH\sim\Delta ADC\left(c.g.c\right)\Rightarrow\widehat{AFH}=\widehat{ADC}=90^o\)
suy ra \(\widehat{HFC}=90^o\) mà \(\widehat{BFC}=90^o\) (do \(F\) thuộc đường tròn \(\left(O\right)\))
suy ra \(B,H,F\) thẳng hàng do đó \(BH\) vuông góc với \(AC\).
Tam giác \(ABC\) có hai đường cao \(AD,BF\) cắt nhau tại \(H\) suy ra \(H\) là trực tâm tam giác \(ABC\).


c) Vì F C H = F D H = 90 o nên tứ giác CHDF nội tiếp đường tròn tâm I đường kính FH
=> IC = ID. Mà OC = OD nên ∆ OCI = ∆ ODI (c.c.c) => COI = DOI
=> OI là phân giác của góc COD
d) Vì OC = CD = OD = R nên ∆ OCD đều => COD = 60o
Có C A D = 1 2 C O D = 30 o = > C F D = 90 o − C A D = 60 o
Xét góc nội tiếp và góc ở tâm cùng chắn cung CD của (I), có
CID = 2CFD = 120o => OIC = OID = C I D 2 = 60 o
Xét góc nội tiếp và góc ở tâm cùng chắn cung CD của (I), có
CID = 2CFD = 120o => OIC = OID = C I D 2 = 60 o
Mặt khác COI = DOI = C O D 2 = 30 o = > O I D + D O I = 90 o = > Δ O I D vuông tại D
Suy ra O I = O D sin 60 o = 2 R 3
Vậy I luôn thuộc đường tròn O ; 2 R 3