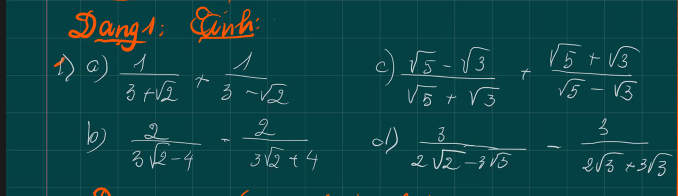
lm hết nhé! Mình cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
24 tháng 3 2022
1. Thơ sáu chữ. 2 khổ thơ
2. Nhân hóa (thời gian chạy qua tóc mẹ). Tác dụng: khiến cho bài văn hay hơn, có cảm xúc hơn.
3. Chạy ở đây nêu lên cảm xúc buồn bã và tiếc nuối của tác giả , ý chỉ thời gian đã trôi qua rất nhanh nên mái tóc của mẹ giờ đây đã bạc màu. Từ chạy ở đây là nghĩa chuyển.
4. Hãy luôn biết ơn, hiếu thảo và yêu thương bố mẹ - người luôn cho ta những điều tốt đẹp nhất
NT
2
N
10 tháng 11 2021
Bài 1:
a. \(R=R1+R2=20+40=60\Omega\)
b. \(I=I1=I2=\dfrac{U}{R}=\dfrac{24}{60}=0,4A\left(R1ntR2\right)\)
Bài 3:
\(P_2>P_1\left(40>10\right)\Rightarrow\) đèn 2 sáng hơn.
19 tháng 12 2016
Bố thì mình không biết nhưng mình biết cô giáo say sưa giảng bài
tớ đng cần gấp ý nên các cậu giúp tớ nhé....tớ camon trc ạaaaaaaa(nếu lm đc hết càng tốt ạ, có lời giải nhé)
31 tháng 1 2021
Ta có :
4 . abc = 400a + 40b + 4c = 399a + 42b + a - 2b + 4c
= 21 ( 19a + 2b ) + ( a - 2b + 4c ) chia hết cho 21
( Do 21 chia hết cho 21 và a - 2b + 4c chia hết cho 21 )
=> 400a + 40b + 4c chia hết cho 21
=> 4 ( 100a + 10b + c ) chia hết cho 21
=> 100a + 10b + c chia hết cho 21
=> abc chia hết cho 21
Vậy nếu a-2b+4c chia hết cho 21 thì abc chia hết cho 21
CH
4
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
Bài 2:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{4^2-2,4^2}=3,2$ (cm)
b.
Áp dụng hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=9.16$
$\Rightarrow AH=12$ (cm)
Áp dụng định lý Pitago:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+9^2}=15$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)
$BC=BH+CH=9+16=25$ (cm)
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
Bài 3:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ (cm)
Áp dụng định lý Pitago:
$15=BC=\sqrt{AB^2+AC^2}=\sqrt{(3a)^2+(4a)^2}=5a$
$\Rightarrow a=3$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{3a.4a}{5a}=2,4a$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(3a)^2-(2,4a)^2}=1,8a=1,8.3=5,4$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{(4a)^2-(2,4a)^2}=3,2a=3,2.3=9,6$ (cm)
17 tháng 12 2018
A = 20 - 21 + 22 - 23 +...+28 - 29
=> 2A = 21 - 22 + 23 - 24 +...+ 29 - 210
=> A+2A = 20 - 210
3A = 1 - 210
=> 210 = 1- 3A
=> x = 10
B
6
ND
Nguyễn Đức Trí
VIP
3 tháng 8 2023
\(10⋮\left(x+5\right)\)
\(\Rightarrow x+5\in\left\{-1;1;-2;2;-5;5;-10;10\right\}\)
\(\Rightarrow x\in\left\{-6;-4;-7;-3;-10;0;-15;5\right\}\left(x\in Z\right)\)
HQ
Hà Quang Minh
Giáo viên
3 tháng 8 2023
Để 10 ⋮ (x+5) thì (x+5) ∈ Ư(10)
⇒ (x+5) ∈ \(\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
⇒ x ∈ {5;0;-3;-4;-6;-7;-10;-15}
a) \(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{9-2}=\dfrac{6}{7}\)
b) \(=\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2+\left(\sqrt{5}+\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{5-2\sqrt{15}+3+5+2\sqrt{15}+3}{5-3}=\dfrac{16}{2}=8\)
c) \(=\dfrac{2\left(3\sqrt{2}+4\right)-2\left(3\sqrt{2}-4\right)}{\left(3\sqrt{2}-4\right)\left(3\sqrt{2}+4\right)}=\dfrac{6\sqrt{2}+8-6\sqrt{2}+8}{18-16}=\dfrac{16}{2}=8\)
d) \(=\dfrac{3\left(2\sqrt{2}+3\sqrt{3}\right)-3\left(2\sqrt{2}-3\sqrt{3}\right)}{\left(2\sqrt{2}-3\sqrt{3}\right)\left(2\sqrt{2}+3\sqrt{3}\right)}=\dfrac{6\sqrt{2}+9\sqrt{3}-6\sqrt{2}+9\sqrt{3}}{8-27}=\dfrac{18\sqrt{3}}{-19}=-\dfrac{18\sqrt{3}}{19}\)
\(a,=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}=\dfrac{6}{3^2-\left(\sqrt{2}\right)^2}=\dfrac{6}{7}\\ b,=\dfrac{2\left(3\sqrt{2}+4\right)-2\left(3\sqrt{2}-4\right)}{\left(3\sqrt{2}-4\right)\left(3\sqrt{2}+4\right)}=\dfrac{6\sqrt{2}+8-6\sqrt{2}+8}{18-16}=\dfrac{16}{2}=8\\ c,=\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2+\left(\sqrt{5}+\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{8-2\sqrt{15}+8+2\sqrt{15}}{2}=\dfrac{16}{2}=8\)
\(d,=\dfrac{3\left(2\sqrt{2}+3\sqrt{3}\right)}{8-27}-\dfrac{3}{5\sqrt{3}}=\dfrac{6\sqrt{2}+9\sqrt{3}}{-19}-\dfrac{\sqrt{3}}{5}\\ =\dfrac{-30\sqrt{2}-45\sqrt{3}-19\sqrt{3}}{95}=\dfrac{-30\sqrt{2}-64\sqrt{2}}{95}\)